【信息论与编码技术】【第2章】 离散信源及其信息测度

信息论与编码理论笔记

第二章 离散信源及其信息测度

2.1 信源的数学模型及分类

无记忆：随机变量之间没有相互依赖
平稳：各随机变量概率分布相同

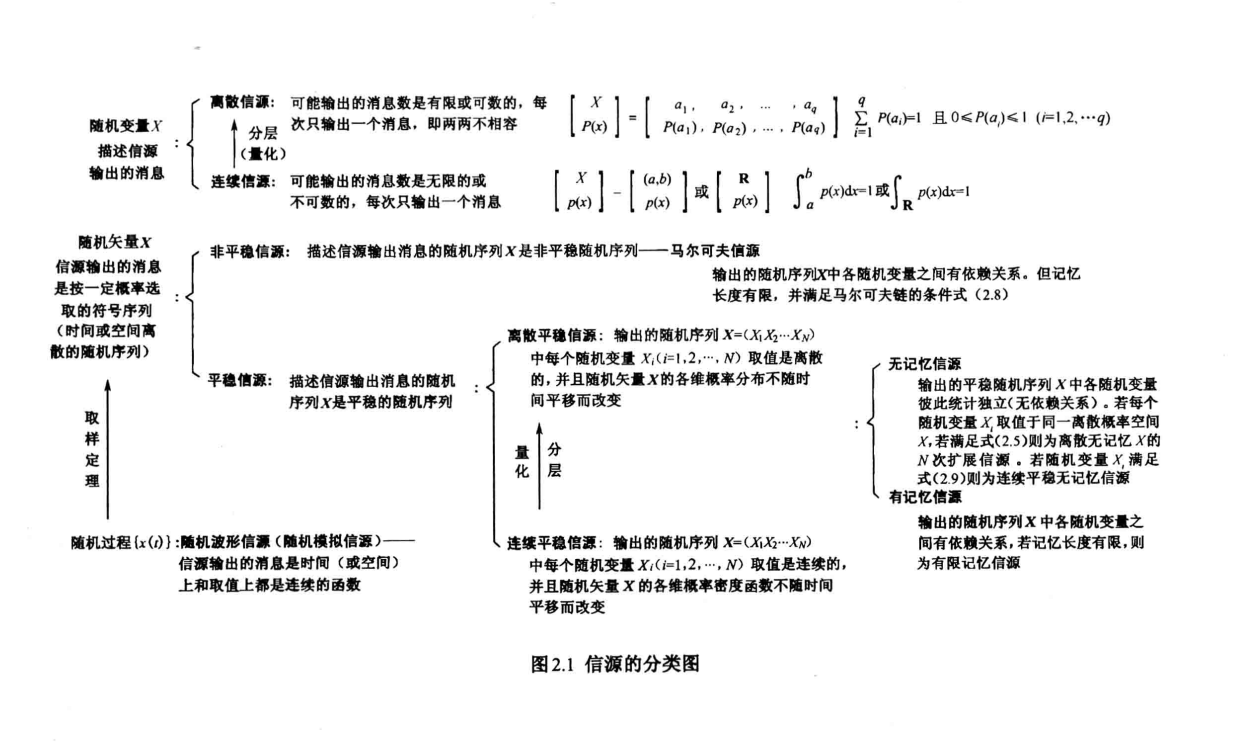
信源是信息的来源，是产生消息或消息序列的源泉。根据信源输出消息的随机性质，可以对信源进行分类。
我们并不关注信源的内部，将其视为一个黑箱，我们只关注信源的输出

2.1.1 随机变量描述信源消息

一维连续信源和一维离散信源
适用于信源可能输出的消息数是有限或可数的，且每次只输出一个消息的情况。
例如，扔一颗质地均匀的骰子，研究下落后朝上一面的点数。

特点：

1. 每次实验只出现一个点数（消息）。
2. 每个点数的出现是随机的。
3. 点数必定为1,2,3,4,5,6中的某一个。

表示：

• 符号集 $A = \{a_1, a_2, a_3, a_4, a_5, a_6\}$ 表示基本消息集合。
• 离散型随机变量 $X$ 描述信源输出的消息，其样本空间为 $A$。
• $X$ 的概率分布即为各消息出现的先验概率，例如 $P(X = a_i) = \frac{1}{6}$。

2.1.2 随机矢量描述信源消息

适用于信源输出的消息由一系列符号序列组成，其中每个符号的出现是不确定的、随机的。

适用场景：

• 中文自然语言作为信源：样本空间 $A$ 为所有汉字和标点符号的集合，汉字和标点符号构成的序列即为中文句子和文章（即消息）。
• 离散化平面灰度图像信源：从 XY 平面空间上来看，每幅黑白灰度画面是一系列空间离散的灰度值符号，空间每一点的符号（灰度值）又是随机的。

特点：

• 信源输出的消息为按一定概率选取的符号序列。
• 时间或空间上离散的一系列随机变量（随机矢量）。

2.1.3 随机过程描述信源消息

适用于信源输出的消息是时间和取值都是连续的情况，例如语音信号、热噪声信号。

特点：

• 信源输出的消息是时间（或空间）上和取值上都是连续的。
• 用随机过程 $\{x(t)\}$ 描述，更一般地说，实际信源输出的消息常常是时间和取值都是连续的。

2.2 离散信源的信息熵

2.2.1 自信息

单符号离散信源中，信息量与不确定性相关。事件发生的不确定性越大，一旦它发生并被接收者收到，消除的不确定性就越大，获得的信息量也就越大。

定义：

$$I(x_i) = \log \frac{1}{P(x_i)} = -\log P(x_i)$$

单位：

• 1 奈特 = $\log_2 e$ 比特 $\approx 1.443$ 比特
• 1 哈特 = $\log_2 10$ 比特 $\approx 3.322$ 比特
  
  

不确定性与发生概率

两个独立事件的联合信息量应等于它们分别的信息量之和。即统计独立信源的信息量等于它们分别的信息量之和。

2.2.1.1 自信息

• 自信息含义：
  • 当事件 xi 发生以前：表示事件 xi 发生的不确定性。
  • 当事件 xi 发生以后：表示事件 xi 所含有（或所提供）的信息量。在无噪信道中，事件 xi 发生后，能正确无误地传输到收信者，所以 I(xi) 可代表接收到消息 xi 后所获得的信息量。这是因为消除了 I(xi) 大小的不确定性，才获得这么大小的信息量。
• 联合自信息
  • 
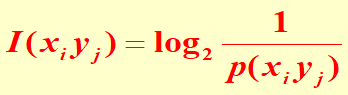
  • 两个随机事件相互独立时，同时发生得到的信息量，等于各自自信息量之和。
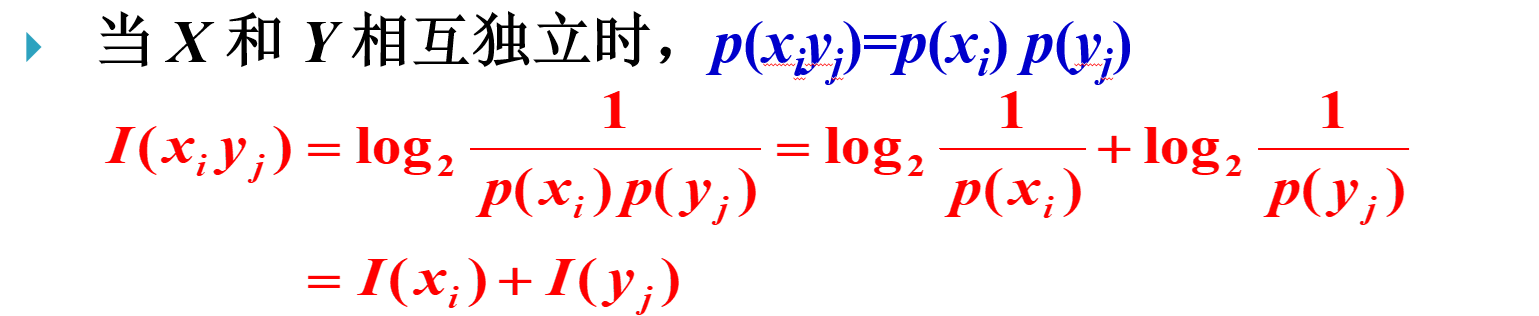
• 条件自信息
  • 设 $y_j$ 条件下，发生 $x_i$ 的条件概率为 $p(x_i / y_j)$，那么它的条件自信息量 $I(x_i / y_j)$ 定义为：

$$I(x_i / y_j) = \log_2 \frac{1}{p(x_i / y_j)}$$

表示在特定条件下（$y_j$ 已定）随机事件 $x_i$ 所带来的信息量。
- 同理，$x_i$ 已知时发生 $y_j$ 的条件自信息量为：

$$I(y_j / x_i) = \log_2 \frac{1}{p(y_j / x_i)}$$

自信息量、条件自信息量和联合自信息量之间的关系

• 联合自信息量 $I(x_i, y_j)$ 可以表示为：
  • 联合自信息量可以分解为自信息量和条件自信息量之和。

$$I(x_i, y_j) = \log_2 \frac{1}{p(x_i) p(y_j / x_i)} = I(x_i) + I(y_j / x_i)$$

$$= \log_2 \frac{1}{p(y_j) p(x_i / y_j)} = I(y_j) + I(x_i / y_j)$$

这些公式展示了条件自信息量、自信息量和联合自信息量之间的关系。

习题 2.4（重点）

问题：设有 12 枚同值硬币，其中有一枚为假币。只知道假币的重量与真币的重量不同，但不知究竟是重还是轻。现采用比较天平左右两边轻重的方法来测量（因无砝码）。为了在天平上称出哪一枚是假币，试问至少必须称多少次？

在信息论的角度下，考虑以下事件：

1. “12枚硬币中，某一枚为假币”该事件发生的概率为 $P = \frac{1}{12}$。
2. “假币的重量比真的轻，或重”该事件发生的概率为 $P = \frac{1}{2}$。

为确定哪一枚是假币，需要消除上述两事件的联合不确定性。由于二者是独立的，因此有：

$$I = \log 12 + \log 2 = \log 24 \text{ 比特}$$

而用天平称时，有三种可能性：重、轻、相等，三者是等概率的，均为 $P = \frac{1}{3}$，因此天平每一次消除的不确定性为 $I = \log 3 \text{ 比特}$。
因此，必须称的次数为：

$$\frac{I_1}{I_2} = \frac{\log 24}{\log 3} \approx 2.9 \text{ 次}$$

因此，至少需称 3 次。

习题2.5

居住在某地区的女孩中有 25% 是大学生，在女大学生中有 75% 是身高 1.6 米以上的，而女孩中身高 1.6 米以上的占总数一半。假如我们得知“身高 1.6 米以上的某女孩是大学生”的消息，问获得多少信息量？

解答：
设：

• $A$ 表示“是大学生”
• $B$ 表示“身高 1.6 米以上”

已知：

• $P(A) = 0.25$
• $P(B|A) = 0.75$
• $P(B) = 0.5$

要求的信息量是 $I(B \to A)$，即已知 $B$ 发生后，关于 $A$ 的不确定性减少量。

根据贝叶斯公式：

$$P(A|B) = \frac{P(B|A) P(A)}{P(B)} = \frac{0.75 \times 0.25}{0.5} = 0.375$$

信息量：

$$I(B \to A) = \log \frac{1}{P(A|B)} = \log \frac{1}{0.375} \approx 1.415 \text{ 比特}$$

2.2.2 信息熵

信息量是一个随机变量
信息熵是信源的平均信息量，是自信息的数学期望。

定义：

$$H(X) = E[I(X)] = -\sum_{i=1}^{n} p(x_i) \log p(x_i)$$

单位：比特/符号（以 2 为底）

意义：

• 表示信源输出后每个消息（符号）所提供的平均信息量。
• 表示信源输出前，信源的平均不确定性。
• 表征信源的随机性。
  

信息熵与平均获得的信息量

信息熵是信源的平均不确定性的描述。在一般情况下它并不等于平均获得的信息量。

• 只有在无噪情况下，接收者才能正确无误地接收到信源所发出的消息，消除 $H(X)$ 大小的平均不确定性，所以获得的平均信息量就等于 $H(X)$。
• 在一般情况下获得的信息量是两熵之差，并不是信源熵本身。

联合熵

联合熵 $H(XY)$ 表示输入随机变量 $X$，经信道传输到达信宿，输出随机变量 $Y$。即收、发双方通信后，整个系统仍然存在的不确定度。

• 两个随机变量 $X, Y$：

$$H(XY) = \sum_{x_i \in X} \sum_{y_j \in Y} p(x_i y_j) \log \frac{1}{p(x_i y_j)}$$

条件熵

条件熵定义：条件熵是在联合符号集合 $XY$ 上的条件自信息的数学期望。

• 在已知 $Y$ 时，$X$ 的条件熵为：

$$H(X / Y) = \sum_{j=1}^{m} \sum_{i=1}^{n} p(x_i y_j) I(x_i / y_j) = \sum_{j=1}^{m} \sum_{i=1}^{n} p(x_i y_j) \log_2 \frac{1}{p(x_i / y_j)}$$

• 已知 $X$ 时，$Y$ 的条件熵为：

$$H(Y / X) = E[I(y_j / x_i)] = \sum_{i=1}^{n} \sum_{j=1}^{m} p(x_i y_j) \log_2 \frac{1}{p(y_j / x_i)}$$

条件熵是一个确定的值。

2.3 信息熵的基本性质和定理

2.3.1 非负性

$$H(X) \geq 0$$

因为 $0 \leq p(x_i) \leq 1$，所以 $\log p(x_i) \leq 0$，从而 $-p(x_i) \log p(x_i) \geq 0$，所以熵 $H(X) \geq 0$。

2.3.2 对称性

黑箱
当变量 $p(x_1), p(x_2), \ldots, p(x_n)$ 的顺序任意互换时，熵函数的值不变。

2.3.3 扩展性

含义：信源的取值增多时，若这些取值对应的概率很小（接近于零），则信源的熵不变。

$$\lim_{p \to 0} H(p, 1-p) = H(1-p)$$

2.3.4 确定性

$$H(1,0) = H(1,0,0) = \ldots = 0$$

当某分量 $p(x_i) = 1$ 时，熵 $H(X) = 0$。

2.3.5 可加性（联合熵 = 信息熵 + 条件熵）

$$H(XY) = H(X) + H(Y|X)$$

2.3.6 上凸性

$$H[\alpha P_1 + (1-\alpha) P_2] > \alpha H(P_1) + (1-\alpha) H(P_2)$$

2.3.7 极值性

离散无记忆信源输出 n 个不同的信息符号，当且仅当各个符号出现概率相等时（即 $p(x_i) = \frac{1}{n}$），熵最大。

2.3.8 最大离散熵定理

定理：离散无记忆信源输出 n 个不同的信息符号，当且仅当各个符号出现概率相等时（即 $p(x_i) = \frac{1}{n}$），熵最大。

2.4 扩展信源

扩展信源
举例：电报系统，发出的是一串有(表示为0)无脉冲(表示为1)的信号系列，表示为010…01.

实际的信源输出的消息是时间或空间上离散的一系列随机变量。这类信源每次输出的不是一个单个的符号，而是一个符号序列。在信源输出的序列中，每一位出现哪个符号都是随机的，而且一般前后符号的出现是有统计依赖关系的。这种信源称为扩展信源/多符号离散信源

2.4.1 离散无记忆信源的扩展

• 把信源输出的序列看成是一组一组发出的。
  • 例1：电报系统中，认为每二个二进制数字组成一组。信源输出由 2 个二进制数字组成的一组组符号。这时可以将它们等效看成一个新的信源，由 4 个符号 00，01，10，11 组成，该信源称为二进制无记忆信源的二次扩展。
  • 例2：把每 3 个二进制数字组成一组，这样长度为 3 的二进制序列就有 8 种不同的序列，等效成一个具有 8 个符号的信源，称为二进制无记忆信源的三次扩展信源。
    二进制无记忆信源的 N 次扩展：把每 N 个二进制数字组成一组，则信源等效成一个具有 2N 个符号的新信源，称为二进制无记忆信源的 N 次扩展信源。

2.4.1 离散无记忆信源的熵

离散无记忆信源的 N 次扩展信源的熵等于离散信源熵的 N 倍，即：

$$H(X^N) = N H(X)$$

2.4.2 离散平稳信源

离散平稳信源的输出随机序列的统计特性与时间的推移无关。

联合熵：

$$H(X_1 X_2 \ldots X_N)$$

1. 二维离散平稳信源的联合熵 $H(X_1X_2)$ 与单符号熵 $H(X)$ 的关系是：

• 答案：B. $H(X_1X_2) \leq 2H(X)$
• 解析：对于二维离散平稳信源，符号之间可能存在依赖关系，因此联合熵 $H(X_1X_2)$ 通常小于或等于两倍的单符号熵 $2H(X)$。只有当两个符号完全独立时，联合熵才等于两倍单符号熵。

条件熵：

$$H(X_{N} | X_1 X_2 \ldots X_{N-1})$$

极限熵：

$$H_\infty = \lim_{N \to \infty} H_N(X) = \lim_{N \to \infty} H(X_N | X_1 X_2 \ldots X_{N-1})$$

2.5 马尔可夫信源

2.5.1 马尔可夫信源的定义

马尔可夫信源的输出符号和所处的状态满足以下条件：

1. 某一时刻信源符号的输出只与此刻信源所处的状态有关，与以前的状态和以前的输出符号都无关。
2. 信源处于某一状态时，再发出一个符号后所处的状态将发生改变。

2.5.2 m 阶马尔可夫信源

m 阶马尔可夫信源的数学模型可由一组信源符号集和一组条件概率确定。当前发出的符号只与前 m 个符号有关，与更前面的符号无关。

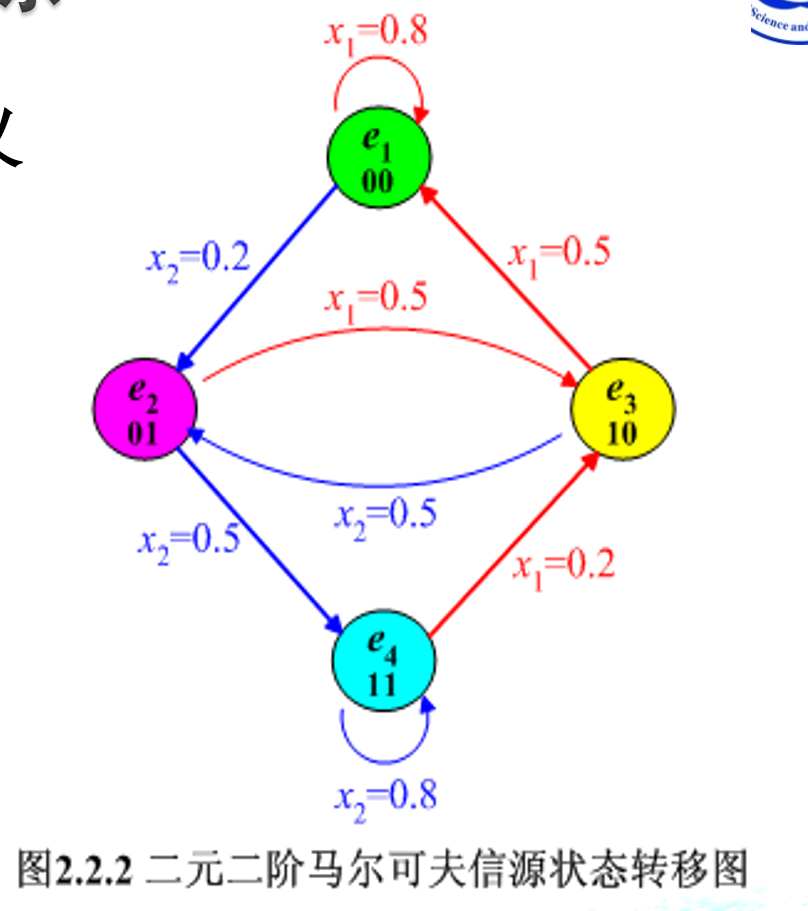
马尔可夫信源的输出符号和所处的状态满足以下两个条件：

1. 无记忆性：
   某一时刻信源符号的输出只与此刻信源所处的状态有关，与以前的状态和以前的输出符号都无关。数学表达式为：

$$P(X_l = x_k \mid S_l = e_i, X_{l-1} = x_{k1}, S_{l-1} = e_j, \ldots) = P(x_k \mid e_i)$$

当具有时齐性时有：

$$P(x_k \mid e_i) = p(x_k \mid e_i)$$

2. 状态转移：
   信源在 $l$ 时刻所处的状态由当前的输出符号和前一时刻 $(l-1)$ 信源的状态唯一确定。数学表达式为：

$$P(S_l = e_j \mid X_l = x_m, S_{l-1} = e_i) = \begin{cases} 0 & \text{if } x_m \neq f(e_i, e_j) \\ 1 & \text{if } x_m = f(e_i, e_j) \end{cases}$$

其中 $f(e_i, e_j)$ 是状态转移函数，表示从状态 $e_i$ 转移到状态 $e_j$ 时输出的符号。

这些条件定义了马尔可夫信源的基本特性，即当前状态只依赖于前一个状态，这种特性使得马尔可夫模型在许多领域中非常有用，尤其是在时间序列分析和自然语言处理中。

2.6 信源剩余度与自然语言的熵

2.6.1 信源剩余度

信源剩余度反映了信源输出符号序列中符号之间的依赖程度，计算公式为：

$$\xi = 1 - \frac{H_\infty}{H_0}$$

其中，$H_\infty$ 是信源的实际熵，$H_0 = \log |A|$ 是最大熵。

2.6.2 自然语言的熵

自然语言如英语、汉语等具有较高的剩余度，意味着符号之间存在较强的依赖关系，信息熵较低。

总结

本章详细介绍了信源的分类、数学模型，以及信息熵的定义、性质和计算方法。通过习题加深了对信息熵和自信息的理解，掌握了如何计算信息量和确定称量次数等实际问题。
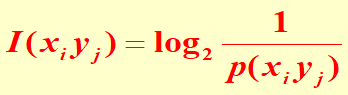
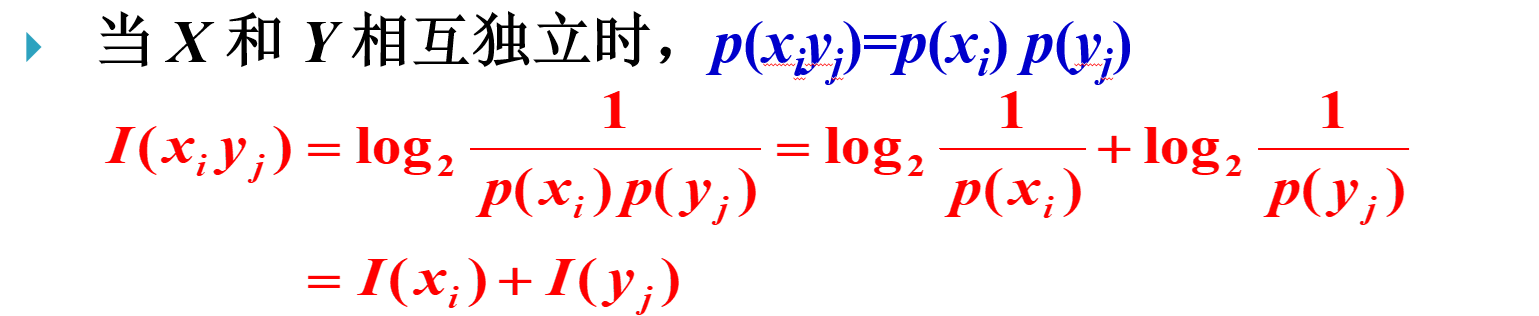