【MIT线性代数】【lec10】 矩阵的四个基本子空间

线性代数第十讲：矩阵的四个基本子空间

一、课程回顾与修正

• 回顾：上一讲中，我们讨论了矩阵的列空间和零空间。
• 修正：在上一讲中，我犯了一个错误。我选择了向量 [1, 1, 2] 和 [2, 2, 5] 作为基，并试图加入 [3, 3, 8] 作为第三个向量。但一位学生指出，这个矩阵的行是线性相关的（有两行相同），因此列向量不可能线性独立。这导致矩阵不可逆，秩为 2，而不是 3。

二、矩阵的四个基本子空间

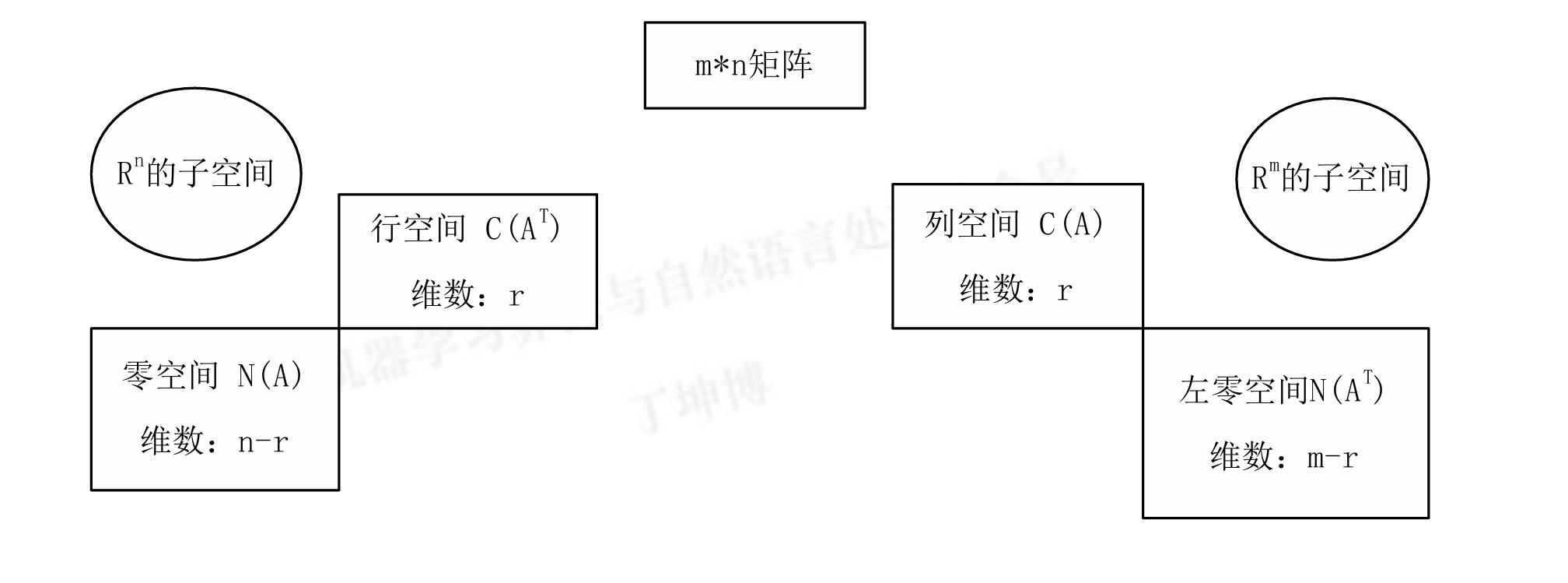
矩阵 $A$ 的四个基本子空间是线性代数的核心内容，它们分别是：

1. 列空间 $C(A)$：由矩阵 $A$ 的列向量的所有线性组合构成。
2. 零空间 $N(A)$：满足 $A\mathbf{x} = \mathbf{0}$ 的所有向量 $\mathbf{x}$ 构成。
3. 行空间：由矩阵 $A$ 的行向量的所有线性组合构成。可以通过转置矩阵 $A^T$ 的列空间来表示。
4. 左零空间 $N(A^T)$：满足 $A^T\mathbf{y} = \mathbf{0}$ 的所有向量 $\mathbf{y}$ 构成，也称为 $A$ 的左零空间。

如何获得空间的全部信息
1.空间的一组基
2.空间的维数

子空间的维度

• 列空间 $C(A)$ 的维度：矩阵 $A$ 的秩 $r$。
• 行空间 的维度：同样为秩 $r$。行空间和列空间的维度相同。
• 零空间 $N(A)$ 的维度：$n - r$，其中 $n$ 是矩阵 $A$ 的列数。
  • 因为秩与主元的个数相同。n-r是自由变量的个数
• 左零空间 $N(A^T)$ 的维度：$m - r$，其中 $m$ 是矩阵 $A$ 的行数。

子空间的关系

• 列空间和零空间位于 $\mathbb{R}^n$ 中，它们的维度之和为 $n$。
• 行空间和左零空间位于 $\mathbb{R}^m$ 中，它们的维度之和为 $m$。

三、子空间的基

• 行变换不会改变行空间，但会改变列空间

1. 列空间的基

• 通过行简化（高斯消元法），找到主元列（pivot columns）。
• 主元列构成列空间的基，其数量即为矩阵的秩 $r$。

2. 零空间的基

• 通过行简化将矩阵 $A$ 化为简化行阶梯形式 $R$。
• 从 $R$ 中读取特殊解（special solutions），这些解构成零空间的基。
• 零空间的维度为 $n - r$，即自由变量的数量。

3. 行空间的基

• 行空间的基可以通过转置矩阵 $A^T$ 的主元列得到。
• 对于矩阵 $A$，其行空间的基是简化行阶梯形式 $R$ 的前 $r$ 行。

4. 左零空间的基

• 通过高斯-若尔当消元法，将矩阵 $[A | I]$ 化为简化行阶梯形式 $[R | E]$。

  • 这种消元法一般用来求解逆矩阵

• 矩阵 $E$ 记录了将 $A$ 化为 $R$ 的所有行操作。

  • 

• 左零空间的基可以通过 $E$ 的最后一行得到，其维度为 $m - r$。

  • 写出EA = R，寻找R中的零行，对应找到E中的线性组合方式，就得到了左零空间的基。

四、示例

考虑矩阵 $A = \begin{bmatrix} 1 & 1 & 1 \\ 2 & 1 & 2 \\ 3 & 2 & 3 \\ 1 & 1 & 1 \end{bmatrix}$：

1. 行简化：

   [1 1 1]
   [2 1 2] -> [0 -1 0] (R2 = R2 - 2R1)
   [3 2 3] -> [0 -1 0] (R3 = R3 - 3R1)
   [1 1 1] -> [0 0 0] (R4 = R4 - R1)

   继续化简：

   [1 1 1]
   [0 1 0] (R2 = -R2)
   [0 -1 0] -> [0 0 0] (R3 = R3 + R2)
   [0 0 0]

   最终得到简化行阶梯形式 $R$：

   [1 0 1]
   [0 1 0]
   [0 0 0]
   [0 0 0]

2. 行空间的基：$R$ 的前两行 [1, 0, 1] 和 [0, 1, 0]。
3. 左零空间的基：通过高斯-若尔当消元法，得到 $E$：

   [1 0 0]
   [2 1 0]
   [3 0 1]
   [1 0 0]

   左零空间的基为 $E$ 的最后一行 [1, 0, -1]。因为这一行对应的结果为0

五、新的向量空间

• 矩阵空间 $M$：将所有 $3 \times 3$ 矩阵视为向量空间。
• 子空间：
  • 上三角矩阵
  • 对称矩阵
  • 对角矩阵（上三角矩阵与对称矩阵的交集）
• 维度计算：
  • 对角矩阵的维度为 3，基为：

$$\begin{bmatrix} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}, \begin{bmatrix} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{bmatrix}, \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$

---

以上是本讲的详细笔记，涵盖了矩阵的四个基本子空间及其基和维度的计算方法。