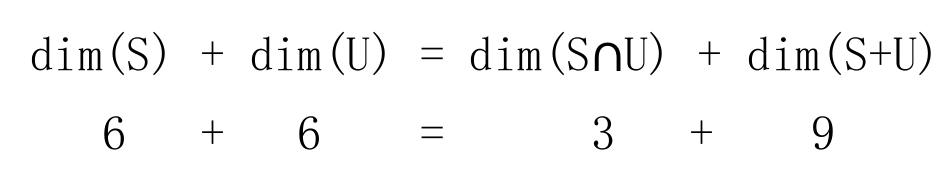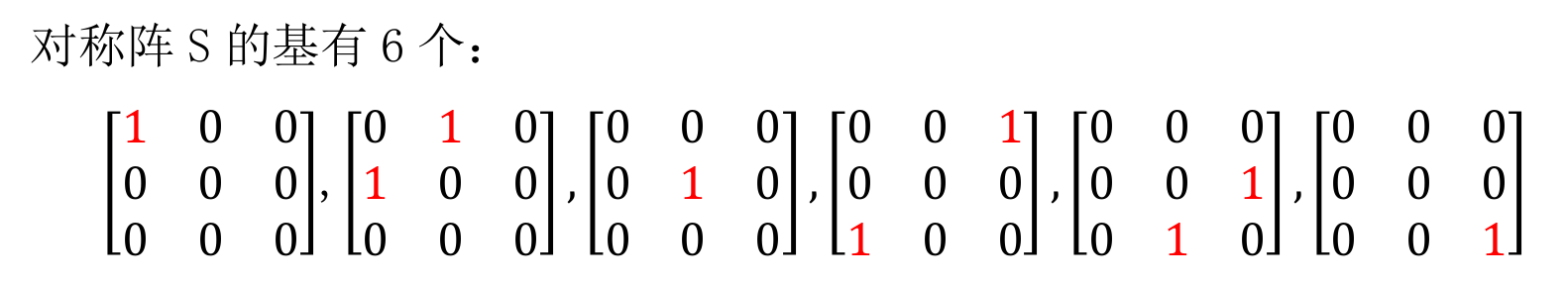【MIT线性代数】【lec11】 向量空间、矩阵秩与图

线性代数第十一讲：矩阵空间、子空间与秩

一、矩阵空间与子空间

1. 矩阵空间 $M$

• 定义：所有 $3 \times 3$ 矩阵构成的空间。
• 性质：可以进行矩阵加法和数乘，但不涉及矩阵乘法。
  • 矩阵也可以视为向量元素
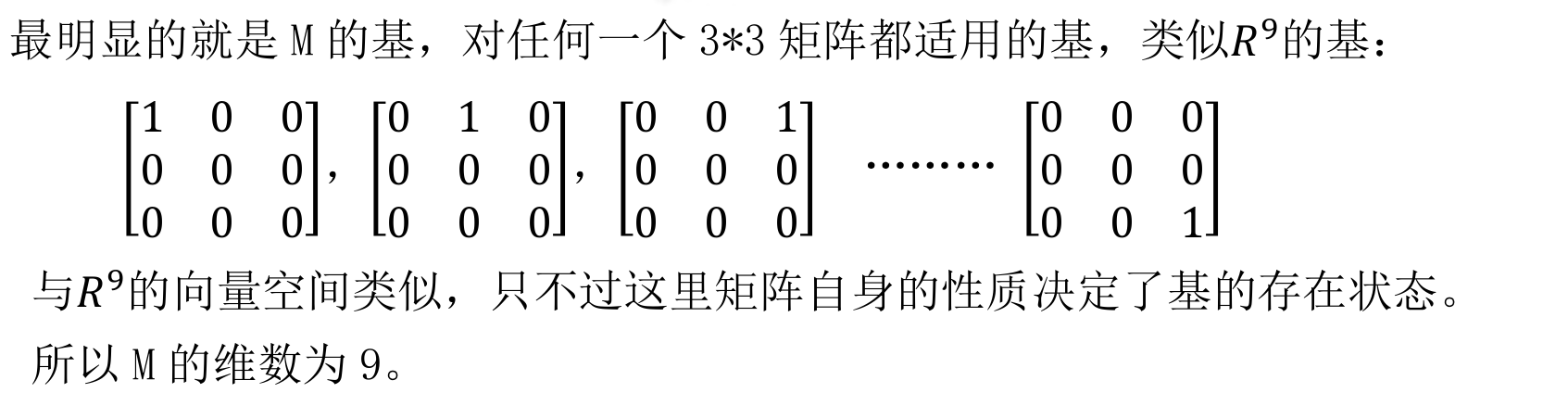
• 维度：9，因为需要 9 个参数来确定一个 $3 \times 3$ 矩阵。
• 标准基：由 9 个矩阵组成，每个矩阵在某个位置有一个 1，其余位置为 0。
  • 

2. 子空间

（1）对称矩阵空间 $S$

• 定义：所有 $3 \times 3$ 对称矩阵构成的子空间。

• 性质：对称矩阵相加仍为对称矩阵。

• 维度：6，因为对称矩阵由对角线上的 3 个元素和对角线上方的 3 个元素决定。

  • 

• 基：由 6 个对称矩阵组成，每个矩阵在对称位置有一个 1，其余位置为 0。

（2）上三角矩阵空间 $U$

• 定义：所有 $3 \times 3$ 上三角矩阵构成的子空间。

• 性质：上三角矩阵相加仍为上三角矩阵。

• 维度：6，因为上三角矩阵由主对角线及其上方的 6 个元素决定。

  • 

• 基：由 6 个上三角矩阵组成，每个矩阵在上三角位置有一个 1，其余位置为 0。

（3）对角矩阵空间 $D$

• 定义：对称且上三角的矩阵，即对角矩阵。

• 性质：对角矩阵相加仍为对角矩阵。

• 维度：3，因为对角矩阵由对角线上的 3 个元素决定。

  • 

• 基：由 3 个对角矩阵组成，每个矩阵在对角线位置有一个 1，其余位置为 0。

3. 子空间的交集与和

• 交集：$S \cap U = D$，即对角矩阵空间。
• 并集：并集不是向量空间，没有研究意义
  • 正如我们在零空间那一节中提到
    • 两个零空间的交集为零空间
    • 两个零空间的并集不是零空间（大概率）
• 和：$S + U = M$，即所有 $3 \times 3$ 矩阵。
• 维度公式：

$$\dim(S + U) = \dim(S) + \dim(U) - \dim(S \cap U)$$

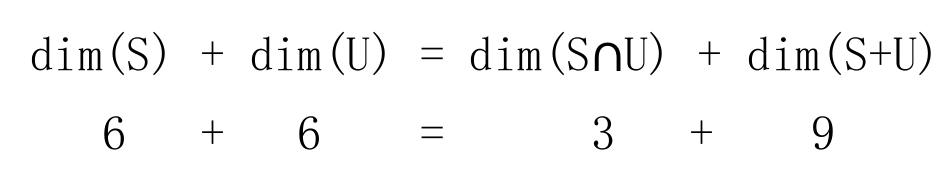
例如，$\dim(S) = 6$，$\dim(U) = 6$，$\dim(S \cap U) = 3$，因此 $\dim(S + U) = 9$。

二、微分方程的解空间

同样的“空间”概念还适用于很多地方，这样的线性空间内元素不一定是向量，矩阵，还可以是方程的解。

1. 方程 $y'' + y = 0$

• 解：$y = \cos(x)$ 和 $y = \sin(x)$ 是解。
• 解空间：由 $\cos(x)$ 和 $\sin(x)$ 张成。
• 维度：2，因为解空间由两个线性无关的函数构成。
• 基：$\{\cos(x), \sin(x)\}$。

三、秩与秩一矩阵

1. 秩的性质

• [[矩阵的秩]]：矩阵中线性无关的行或列的最大数目。
• 性质：秩不超过矩阵的行数和列数。

2. 秩一矩阵

• 定义：秩为 1 的矩阵。
• 性质：秩一矩阵可以表示为一个列向量与一个行向量的乘积。
  • 

$$A = \mathbf{u} \mathbf{v}^T$$

其中 $\mathbf{u}$ 是列向量，$\mathbf{v}^T$ 是行向量。

• 应用：秩一矩阵是构建其他矩阵的基本单元。秩一矩阵的另外一个优点是它可以“搭建”其他矩阵，比如秩为4的矩阵，通过四个秩一矩阵就能搭建出来。具体过程类似于矩阵乘法中的“列乘行”形式，通过一列一行搭出一个矩阵。

3. 秩与子空间

• 秩四矩阵：所有 $5 \times 17$ 的秩四矩阵不能构成子空间，因为两个秩四矩阵的和可能秩更高。

四、具体[[子空间]]示例

1. 四维空间中的子空间 $S$

• 定义：所有满足 $v_1 + v_2 + v_3 + v_4 = 0$ 的向量 $\mathbf{v}$ 构成的子空间。
• 性质：是子空间，因为满足线性组合的性质。
• 维度：3，因为有 4 个变量和 1 个约束条件。
• 基：通过求解齐次线性方程组得到三个线性无关的解向量。

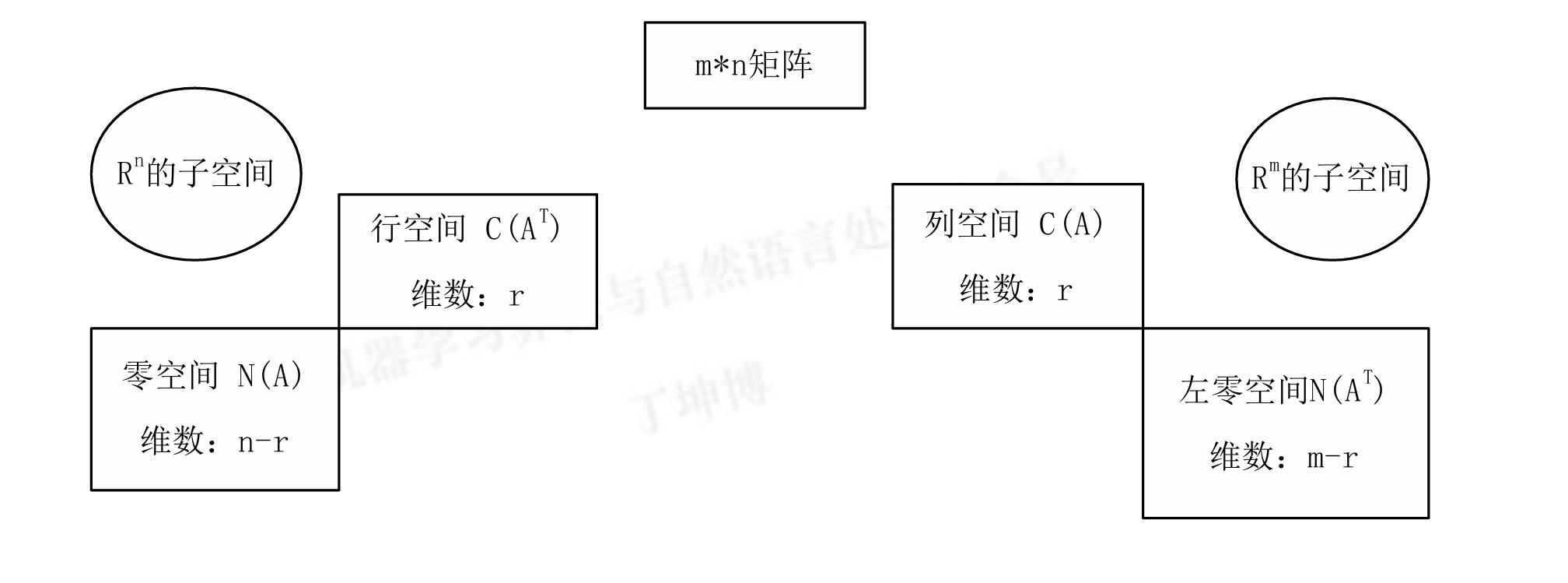
2. 矩阵的四基本子空间

• 矩阵：$A = \begin{bmatrix} 1 & 1 & 1 & 1 \end{bmatrix}$
• 秩：1
• 四基本子空间：
  • 列空间 $C(A)$：维度为 1，基为 $\{[1]\}$。
  • 零空间 $N(A)$：维度为 3，基为 $\{\begin{bmatrix} -1 \\ 1 \\ 0 \\ 0 \end{bmatrix}, \begin{bmatrix} -1 \\ 0 \\ 1 \\ 0 \end{bmatrix}, \begin{bmatrix} -1 \\ 0 \\ 0 \\ 1 \end{bmatrix}\}$。
  • 行空间 $C(A^T)$：维度为 1，基为 $\{\begin{bmatrix} 1 & 1 & 1 & 1 \end{bmatrix}\}$。
  • 左零空间 $N(A^T)$：维度为 0，基为空集。

五、图与小世界现象

1. 图的定义

• 定义：图由节点（nodes）和连接节点的边（edges）组成。
• 示例：一个包含 5 个节点和 6 条边的图。

2. 小世界现象

• 六度分隔：在社交网络中，任意两人之间通常通过不超过六步的中间人连接。
• 数学意义：研究图中节点间的最短路径，理解复杂网络的结构和性质。
• 应用：
  • 社交网络：例如，每个人可以被视为一个节点，朋友关系可以被视为边。
  • 互联网：网站可以被视为节点，链接可以被视为边。
  • 数学问题：通过添加少量“捷径”，可以显著减少节点间的距离。

矩阵空间练习；秩1；小世界图

问题 11.1：[可选]（3.5 #41.《线性代数导论》：Strang）

题目要求：

1. 将3×3单位矩阵表示为其他五个置换矩阵的线性组合。
2. 证明这五个置换矩阵是线性无关的。
3. 说明这五个置换矩阵构成了所有行和与列和均相等的3×3矩阵子空间的一个基。

解释与解答

1. 将3×3单位矩阵表示为其他五个置换矩阵的线性组合

3×3单位矩阵 $I$ 为：

$$I = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$

3×3置换矩阵：所有3×3的置换矩阵共有6个，它们是单位矩阵的所有可能的行（或列）置换。这6个置换矩阵分别为：

$$P_1 = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}, \quad P_2 = \begin{bmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix}, \quad P_3 = \begin{bmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{bmatrix}$$

$$P_4 = \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{bmatrix}, \quad P_5 = \begin{bmatrix} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{bmatrix}, \quad P_6 = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{bmatrix}$$

题目要求将单位矩阵 $I$ 表示为这6个置换矩阵中其他5个的线性组合。假设我们选择 $P_2, P_3, P_4, P_5, P_6$，则需要找到系数 $c_1, c_2, c_3, c_4, c_5$，使得：

$$I = c_1 P_2 + c_2 P_3 + c_3 P_4 + c_4 P_5 + c_5 P_6$$

2. 证明这五个置换矩阵是线性无关的

假设某个线性组合为：

$$c_1 P_2 + c_2 P_3 + c_3 P_4 + c_4 P_5 + c_5 P_6 = 0$$

我们需要证明 $c_1 = c_2 = c_3 = c_4 = c_5 = 0$。为此，可以检查矩阵的特定元素。例如，考虑矩阵的对角线元素和非对角线元素，通过这些元素的线性组合必须为零，可以推导出所有系数都为零。

3. 这五个置换矩阵构成了所有行和与列和均相等的3×3矩阵子空间的一个基

行和与列和均相等的3×3矩阵子空间：这个子空间包含所有3×3矩阵，其中每一行的和与每一列的和都相等。例如，单位矩阵 $I$ 的行和与列和均为1，而全1矩阵的行和与列和均为3。

基的定义：基是一组线性无关的向量（或矩阵），它们的线性组合可以生成整个子空间。题目中提到的五个置换矩阵是线性无关的，并且它们的线性组合可以生成所有行和与列和均相等的3×3矩阵子空间。

具体解答

表示单位矩阵为线性组合：
通过观察和计算，可以找到合适的系数。例如：

$$I = P_2 + P_3 + P_4 - P_5 - P_6$$

证明线性无关性：
假设：

$$c_1 P_2 + c_2 P_3 + c_3 P_4 + c_4 P_5 + c_5 P_6 = 0$$

通过检查矩阵的对角线和非对角线元素，可以推导出 $c_1 = c_2 = c_3 = c_4 = c_5 = 0$。

基的验证：
这五个置换矩阵是线性无关的，并且它们的线性组合可以生成所有行和与列和均相等的3×3矩阵子空间。因此，它们构成了该子空间的一个基。

问题 11.2：（3.6 #31.）

题目要求：

1. 找出所有满足 $AX = 0$ 的3×3矩阵 $X$。
2. 找出所有可以表示为 $AX$ 形式的3×3矩阵。
3. 确定操作 $AX$ 的“零空间”和“列空间”的维度，并解释它们的维度之和为9的原因。

解释与解答

1. 找出所有满足 $AX = 0$ 的3×3矩阵 $X$

矩阵 $A$：

$$A = \begin{bmatrix} 1 & -1 & 0 \\ -1 & 1 & 0 \\ 0 & -1 & 1 \end{bmatrix}$$

零空间的定义：零空间 $N(A)$ 是所有满足 $AX = 0$ 的矩阵 $X$ 的集合。

求解 $AX = 0$：
通过行简化或其他方法，可以发现 $A$ 的行是线性相关的，其秩为2。因此，$A$ 的零空间的维度为 $3 - 2 = 1$。零空间的一个基向量为：

$$\begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}$$

因此，满足 $AX = 0$ 的矩阵 $X$ 的列向量必须是这个基向量的倍数。所以，$X$ 必须具有以下形式：

$$X = \begin{bmatrix} a & b & c \\ a & b & c \\ a & b & c \end{bmatrix}$$

2. 找出所有可以表示为 $AX$ 形式的3×3矩阵

列空间的定义：列空间 $C(A)$ 是所有可以表示为 $AX$ 形式的矩阵的集合。

求解 $AX$：
任何形式为 $AX$ 的矩阵的列向量都是 $A$ 的列向量的线性组合。因此，一个矩阵具有 $AX$ 的形式，当且仅当它的每一列的和都为0。所以，可以表示为 $AX$ 形式的矩阵 $B$ 必须具有以下形式：

$$B = \begin{bmatrix} a & b & c \\ d & -a - d & e \\ f & -b - e & -c - f \end{bmatrix}$$

3. 确定操作 $AX$ 的“零空间”和“列空间”的维度，并解释它们的维度之和为9的原因

零空间的维度：零空间 $N(A)$ 的维度为3，因为 $A$ 的秩为2，而 $A$ 是一个3×3矩阵。

列空间的维度：列空间 $C(A)$ 的维度为6，因为 $A$ 的秩为2，而 $A$ 是一个3×3矩阵，所以 $C(A)$ 的维度为 $3 \times 3 - 3 = 6$。

维度之和：零空间的维度与列空间的维度之和为 $3 + 6 = 9$，这等于输入空间 $M$ 的维度。这是因为 $M$ 是所有3×3矩阵的空间，其维度为 $3 \times 3 = 9$。

具体解答

a) 满足 $AX = 0$ 的矩阵 $X$：

$$X = \begin{bmatrix} a & b & c \\ a & b & c \\ a & b & c \end{bmatrix}$$

b) 可以表示为 $AX$ 形式的矩阵 $B$：

$$B = \begin{bmatrix} a & b & c \\ d & -a - d & e \\ f & -b - e & -c - f \end{bmatrix}$$

c) 零空间和列空间的维度：

• 零空间的维度为3。
• 列空间的维度为6。
• 它们的维度之和为9，等于输入空间 $M$ 的维度。