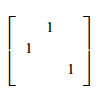【MIT线性代数】【lec4】分解为a = lu

线性代数第四讲：矩阵乘法与逆矩阵

一、矩阵乘法与逆矩阵

1. 矩阵乘法的逆

• 问题：已知矩阵 $A$ 和 $B$ 的逆矩阵，求 $AB$ 的逆矩阵。
• 结论：$(AB)^{-1} = B^{-1}A^{-1}$。
  • 验证：

$$AB \times B^{-1}A^{-1} = A(BB^{-1})A^{-1} = AIA^{-1} = AA^{-1} = I$$

同理，从右侧验证：

$$B^{-1}A^{-1} \times AB = B^{-1}(A^{-1}A)B = B^{-1}IB = B^{-1}B = I$$

2. 矩阵转置的逆

• 问题：已知矩阵 $A$ 的逆矩阵，求 $A^T$ 的逆矩阵。
• 结论：$(A^T)^{-1} = (A^{-1})^T$。
  • 验证：

$$A^T \times (A^{-1})^T = (A^{-1}A)^T = I^T = I$$

二、高斯消元法与矩阵分解

1. 高斯消元法

• 目标：通过行操作将矩阵 $A$ 化为上三角矩阵 $U$。
• 步骤：
  1. 使用消元矩阵 $E_{21}$ 将第二行的第一个元素化为零。
  2. 使用消元矩阵 $E_{31}$ 将第三行的第一个元素化为零。
  3. 使用消元矩阵 $E_{32}$ 将第三行的第二个元素化为零。
• 矩阵形式：

$$E_{32}E_{31}E_{21}A = U$$

2. 矩阵分解 $A = LU$

• 定义：将矩阵 $A$ 分解为下三角矩阵 $L$ 和上三角矩阵 $U$ 的乘积。
• 构造方法：
  • $U$ 是通过高斯消元法得到的上三角矩阵。
  • $L$ 是消元矩阵的逆矩阵的乘积，即 $L = E_{21}^{-1}E_{31}^{-1}E_{32}^{-1}$。
• 示例：
  • 矩阵 $A$：

$$A = \begin{bmatrix} 2 & 1 \\ 8 & 7 \end{bmatrix}$$

• 消元步骤：
  1. $E_{21}$ 将第二行的第一个元素化为零：

$$E_{21} = \begin{bmatrix} 1 & 0 \\ -4 & 1 \end{bmatrix}$$

$$E_{21}A = \begin{bmatrix} 2 & 1 \\ 0 & 3 \end{bmatrix} = U$$

2. $L$ 是 $E_{21}$ 的逆矩阵：

$$L = E_{21}^{-1} = \begin{bmatrix} 1 & 0 \\ 4 & 1 \end{bmatrix}$$

3. 验证：

$$A = LU = \begin{bmatrix} 1 & 0 \\ 4 & 1 \end{bmatrix} \begin{bmatrix} 2 & 1 \\ 0 & 3 \end{bmatrix} = \begin{bmatrix} 2 & 1 \\ 8 & 7 \end{bmatrix}$$

3. 矩阵分解的扩展形式 $A = LDU$

• 定义：将矩阵 $A$ 分解为下三角矩阵 $L$、对角矩阵 $D$ 和上三角矩阵 $U$ 的乘积。
• 示例：
  • 矩阵 $A$：

$$A = \begin{bmatrix} 2 & 1 \\ 8 & 7 \end{bmatrix}$$

• 分解：

$$L = \begin{bmatrix} 1 & 0 \\ 4 & 1 \end{bmatrix}, \quad D = \begin{bmatrix} 2 & 0 \\ 0 & 3 \end{bmatrix}, \quad U = \begin{bmatrix} 1 & 0.5 \\ 0 & 1 \end{bmatrix}$$

$$A = LDU = \begin{bmatrix} 1 & 0 \\ 4 & 1 \end{bmatrix} \begin{bmatrix} 2 & 0 \\ 0 & 3 \end{bmatrix} \begin{bmatrix} 1 & 0.5 \\ 0 & 1 \end{bmatrix}$$

三、矩阵分解的计算复杂度

1. 消元法的计算量

• 问题：计算矩阵 $A$ 的消元步骤所需的计算量。
• 分析：
  • 第一步：处理 $n \times n$ 矩阵，计算量约为 $n^2$。
  • 第二步：处理 $(n-1) \times (n-1)$ 矩阵，计算量约为 $(n-1)^2$。
  • 以此类推，总计算量为：

$$n^2 + (n-1)^2 + (n-2)^2 + \dots + 1^2$$

• 近似结果：总计算量约为 $\frac{1}{3}n^3$。

2. 右端向量 $b$ 的计算量

• 问题：计算右端向量 $b$ 的消元步骤所需的计算量。
• 结论：总计算量约为 $n^2$。

四、置换矩阵

1. 置换矩阵的定义

• 定义：置换矩阵 $P$ 是通过交换单位矩阵 $I$ 的行得到的矩阵。
• 性质：
  • 置换矩阵的逆矩阵等于其转置矩阵，即 $P^{-1} = P^T$。
  • 置换矩阵的乘积仍然是置换矩阵。

2. 置换矩阵的数量

• 数量：对于 $n \times n$ 矩阵，有 $n!$ 个置换矩阵。
• 示例：
  • 3×3 置换矩阵：

$$P = \begin{bmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$

$$P^{-1} = P^T = \begin{bmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$

五、总结

• 矩阵乘法与逆矩阵：
  • $(AB)^{-1} = B^{-1}A^{-1}$
  • $(A^T)^{-1} = (A^{-1})^T$
• 高斯消元法与矩阵分解：
  • $A = LU$，其中 $L$ 是下三角矩阵，$U$ 是上三角矩阵。
  • $A = LDU$，其中 $L$ 是下三角矩阵，$D$ 是对角矩阵，$U$ 是上三角矩阵。
• 计算复杂度：
  • 消元法的计算量约为 $\frac{1}{3}n^3$。
  • 右端向量 $b$ 的计算量约为 $n^2$。
• 置换矩阵：
  • 置换矩阵的逆矩阵等于其转置矩阵。
  • 对于 $n \times n$ 矩阵，有 $n!$ 个置换矩阵。