线性代数笔记 - 第八讲:解线性方程组 Ax=b
一、课程主题
本次课程的目标是完全解决线性方程组 Ax=b 的问题,包括判断方程组是否有解,以及如何找到所有解。
二、解线性方程组的步骤
(一)判断方程组是否有解
-
消元法(Elimination)
- 对增广矩阵 [A∣b] 进行行消元操作,判断是否会出现矛盾的方程(如 0=c,其中 c=0)。
- 如果出现矛盾方程,则方程组无解;否则,方程组有解。
-
条件:b 必须在 A 的列空间中
- 方程组 Ax=b 有解的条件是 b 必须是 A 的列的线性组合,即 b 在 A 的列空间中。
- 如果某些行的线性组合为零行,则 b 的对应组合也必须为零。
(二)求解方程组
- 找到一个特解(Particular Solution)
- 方法:将所有自由变量设为零,解出主元变量。
- 示例:
A=⎣⎢⎡1232462682810⎦⎥⎤,b=⎣⎢⎡156⎦⎥⎤
- 增广矩阵 $[A|b]$:
⎣⎢⎡1232462682810∣∣∣156⎦⎥⎤
- 消元后得到:
⎣⎢⎡100200220240∣∣∣130⎦⎥⎤
- 自由变量:$x_2, x_4$;主元变量:$x_1, x_3$。
- 设 $x_2 = 0, x_4 = 0$,解方程:
{x1+2x3=12x3=3
- 解得:$x_3 = \frac{3}{2}$,$x_1 = 1 - 2 \times \frac{3}{2} = -2$。
- 特解:$\mathbf{x}_p = \begin{bmatrix} -2 \\ 0 \\ \frac{3}{2} \\ 0 \end{bmatrix}$。
- 找到零空间的特解(Null Space Solutions)
- 方法:解 Ax=0,找到零空间的基向量。
- 示例:
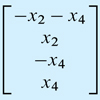
xn=c1⎣⎢⎢⎢⎡−2100⎦⎥⎥⎥⎤+c2⎣⎢⎢⎢⎡20−21⎦⎥⎥⎥⎤
- 其中,$c_1$ 和 $c_2$ 是任意常数。
- 完整解(Complete Solution)
x=xp+xn=⎣⎢⎢⎢⎡−20230⎦⎥⎥⎥⎤+c1⎣⎢⎢⎢⎡−2100⎦⎥⎥⎥⎤+c2⎣⎢⎢⎢⎡20−21⎦⎥⎥⎥⎤
三、矩阵的秩(Rank)与解的性质
-
秩的定义
- 矩阵的秩 r 是矩阵中主元的数量。
- 秩 r 满足 r≤min(m,n),其中 m 是行数,n 是列数。
-
秩与解的关系
- 满列秩(Full Column Rank, r=n):
- 每列都有主元,无自由变量。
- 零空间只有零向量。
- 方程组 Ax=b 有唯一解(如果存在)。
- 满行秩(Full Row Rank, r=m):
- 每行都有主元,无零行。
- 方程组 Ax=b 有解(可能有多个解)。
- 方阵且满秩(Square Matrix, r=m=n):
- 矩阵可逆,零空间只有零向量。
- 方程组 Ax=b 有唯一解。
- 秩小于 m 和 n(r<m,r<n):
四、总结
本次课程通过具体的矩阵和方程组示例,详细介绍了如何判断线性方程组 Ax=b 是否有解,并通过消元法找到特解和零空间的特解,从而得到完整解。矩阵的秩是判断解的性质的关键,它决定了方程组是否有解、解的唯一性以及零空间的结构。这些内容为后续学习线性代数中的矩阵理论和应用奠定了基础。