【MIT线性代数】【lec12】 图与矩阵

线性代数应用：图与矩阵

1. 线性代数的应用背景

• 线性代数中的矩阵并非随意构造，而是来源于实际应用。例如，化学教授通过矩阵分析化学反应，利用行简化（row reduction）来理解复杂的化学反应过程。
• 在Mathworks（Matlab的开发公司）举办的活动中，讨论了线性代数在多个领域的应用。

2. 图（Graph）与矩阵

• 图的定义：图由节点（nodes）和边（edges）组成。例如，可以考虑所有网站、电话或人的图。
• 示例图：构造一个包含4个节点和5条边的简单图。节点编号为1、2、3、4，边的方向分别为1→2、2→3、1→3、1→4、3→4。
• 矩阵的构造：根据图的结构，构造与之对应的矩阵，称为关联矩阵（Incidence Matrix）。矩阵的行对应边，列对应节点。矩阵的元素表示边与节点的关系，具体为：
  • 如果边从节点出发，对应位置为-1；
  • 如果边指向节点，对应位置为+1；
  • 如果边与节点无关，对应位置为0。

3. 关联矩阵的性质

• 矩阵维度：对于上述图，矩阵维度为5×4（5条边，4个节点）。
• 稀疏性：矩阵中每行只有两个非零元素（一个-1和一个+1），因此矩阵非常稀疏。
• 结构：矩阵的结构反映了图的结构，例如，矩阵中的行对应边，列对应节点。

4. 矩阵的零空间（Null Space）

• 零空间的定义：零空间包含所有满足方程 $Ax=0$ 的向量 $x$。
• 求解零空间：通过解方程 $Ax=0$，找到零空间中的向量。对于上述矩阵，零空间的维度为1，一个基向量为 $[1, 1, 1, 1]$。这意味着所有节点的电势（potentials）相同时，电势差为零，电流不会流动。
• 物理意义：零空间中的向量表示电势可以任意增加或减少一个常数，而不会影响电流的流动。

5. 矩阵的秩（Rank）

• 秩的定义：矩阵的秩是其列向量中线性无关的个数。
• 计算秩：对于上述矩阵，秩为3。这意味着矩阵中有3个线性无关的列。

6. 矩阵的转置零空间（Null Space of $A^T$）

• 方程 $A^T y = 0$：这是应用数学中最基本的方程之一，表示电流满足基尔霍夫电流定律（Kirchhoff’s Current Law, KCL）。
• 基尔霍夫电流定律：该定律指出，流入节点的电流等于流出节点的电流。例如，对于节点1，方程为 $-y_1 - y_3 - y_4 = 0$。
• 求解 $A^T y = 0$：通过分析图的结构，可以找到满足该方程的电流向量 $y$。例如，可以找到两个线性无关的解，分别对应于图中的两个环路。

7. 矩阵的行空间（Row Space）与列空间（Column Space）

• 行空间的维度：矩阵的行空间的维度等于其秩，即3。
• 列空间的维度：矩阵的列空间的维度也等于其秩，即3。

8. 欧拉公式（Euler’s Formula）

• 公式：对于任意图，节点数（n）减去边数（m）加上环路数（l）等于1，即 $n - m + l = 1$。
• 验证：通过分析图的结构，可以验证该公式。例如，对于上述图，节点数为4，边数为5，环路数为2，满足 $4 - 5 + 2 = 1$。

9. 应用数学的基本方程

• 电势差：电势差 $E$ 由矩阵 $A$ 与电势向量 $x$ 的乘积给出，即 $E = Ax$。
• 电流：电流 $y$ 由电势差 $E$ 通过欧姆定律（Ohm’s Law）给出，即 $y = CE$。
• 基尔霍夫电流定律：电流 $y$ 满足基尔霍夫电流定律，即 $A^T y = 0$。

10. 矩阵 $A^T C A$ 的性质

• 对称性：矩阵 $A^T C A$ 是对称矩阵。
• 物理意义：该矩阵在应用数学中具有重要意义，例如在电路分析中，它与系统的平衡方程有关。

总结

• 本节课通过图与矩阵的关系，展示了线性代数在实际应用中的重要性。
• 关联矩阵的零空间、秩、转置零空间等概念在电路分析、网络流等领域具有重要的物理意义。
• 欧拉公式揭示了图的结构与节点、边、环路之间的关系。
• 应用数学的基本方程通过矩阵 $A$、$A^T$ 和欧姆定律将电势、电势差和电流联系起来。

图、网络与关联矩阵的练习

问题 12.1：（8.2 #1.《线性代数导论》：Strang）

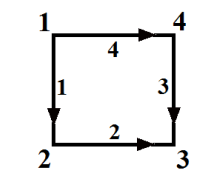
写出下图所示的正方形图的4×4关联矩阵 $A$。（提示：第一行在第1列有-1，在第2列有+1。）哪些向量 $(x_1, x_2, x_3, x_4)$ 在 $A$ 的零空间中？如何判断 $(1,0,0,0)$ 不在 $A$ 的行空间中？

解答：

关联矩阵 $A$：

$$A = \begin{bmatrix} -1 & 1 & 0 & 0 \\ 0 & -1 & 1 & 0 \\ 0 & 0 & -1 & 1 \\ 1 & 0 & 0 & -1 \end{bmatrix}$$

求零空间：解方程 $Ax = 0$：

$$\begin{bmatrix} -1 & 1 & 0 & 0 \\ 0 & -1 & 1 & 0 \\ 0 & 0 & -1 & 1 \\ 1 & 0 & 0 & -1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}$$

逐行分析：

1. $x_2 - x_1 = 0$ ⇒ $x_2 = x_1$
2. $x_3 - x_2 = 0$ ⇒ $x_3 = x_2 = x_1$
3. $x_4 - x_3 = 0$ ⇒ $x_4 = x_3 = x_2 = x_1$
4. $x_1 - x_4 = 0$ ⇒ $x_1 = x_4$

因此，零空间中的向量形式为 $(a, a, a, a)$，其中 $a$ 是任意常数。

判断 $(1,0,0,0)$ 不在 $A$ 的行空间中：
行空间是零空间的正交补空间。由于 $(1,0,0,0)$ 与零空间中的向量 $(a, a, a, a)$ 不正交（因为它们的点积不为零），所以 $(1,0,0,0)$ 不在 $A$ 的行空间中。

问题 12.2：（8.2 #7.）

继续使用问题1中的网络，假设电导矩阵为：

$$C = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$

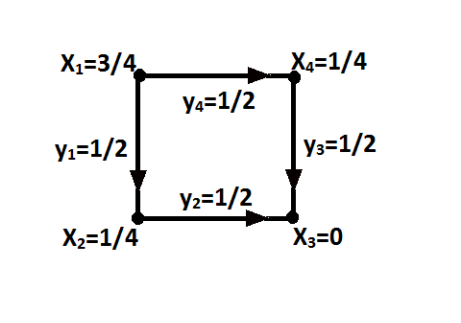
计算矩阵乘积 $A^TCA$。对于 $f = (1, 0, -1, 0)$，求解方程 $A^TCAx = f$。在正方形图上标出对应的电势 $x$ 和电流 $y = -CAx$，其中电流源 $f$ 从节点1流入，从节点3流出。

解答：

关联矩阵 $A$：

$$A = \begin{bmatrix} -1 & 1 & 0 & 0 \\ 0 & -1 & 1 & 0 \\ 0 & 0 & -1 & 1 \\ 1 & 0 & 0 & -1 \end{bmatrix}$$

计算 $A^TCA$：

$$A^T = \begin{bmatrix} -1 & 0 & 0 & 1 \\ 1 & -1 & 0 & 0 \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 1 & -1 \end{bmatrix}$$

$$A^TCA = \begin{bmatrix} -1 & 0 & 0 & 1 \\ 1 & -1 & 0 & 0 \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 1 & -1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} -1 & 1 & 0 & 0 \\ 0 & -1 & 1 & 0 \\ 0 & 0 & -1 & 1 \\ 1 & 0 & 0 & -1 \end{bmatrix}$$

计算过程：

$$A^TCA = \begin{bmatrix} 2 & -1 & 0 & -1 \\ -1 & 3 & -1 & 0 \\ 0 & -1 & 3 & -1 \\ -1 & 0 & -1 & 2 \end{bmatrix}$$

求解方程 $A^TCAx = f$：

$$A^TCAx = \begin{bmatrix} 2 & -1 & 0 & -1 \\ -1 & 3 & -1 & 0 \\ 0 & -1 & 3 & -1 \\ -1 & 0 & -1 & 2 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} = \begin{bmatrix} 1 \\ 0 \\ -1 \\ 0 \end{bmatrix}$$

通过行简化增广矩阵：

$$\begin{bmatrix} 2 & -1 & 0 & -1 & | & 1 \\ -1 & 3 & -1 & 0 & | & 0 \\ 0 & -1 & 3 & -1 & | & -1 \\ -1 & 0 & -1 & 2 & | & 0 \end{bmatrix}$$

假设 $x_3 = 0$（表示节点3接地），解得：

$$x = \begin{bmatrix} 3/4 \\ 1/4 \\ 0 \\ 1/4 \end{bmatrix}$$

计算电流 $y = -CAx$：

$$y = -CAx = -\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 3/4 \\ 1/4 \\ 0 \\ 1/4 \end{bmatrix} = \begin{bmatrix} -3/4 \\ -1/2 \\ 0 \\ -1/4 \end{bmatrix}$$

在正方形图上标出电势和电流：

• 节点电势 $x$：$(3/4, 1/4, 0, 1/4)$
• 边上的电流 $y$：$(-3/4, -1/2, 0, -1/4)$
  

---