【MIT线性代数】【lec13】第一单元复习

第一部分：线性方程组的解法与LU分解

课程主题

• 线性方程组的解法
• 矩阵的LU分解
• 线性系统的完整解

问题描述

给定一个3x3矩阵 $A$，其中最后一个元素是参数 $k$。矩阵 $A$ 如下：

$$A = \begin{bmatrix} 1 & 1 & 1 \\ 1 & 2 & 3 \\ 3 & 4 & k \\ \end{bmatrix}$$

考虑方程组 $A \mathbf{x} = \begin{bmatrix} 2 \\ 3 \\ 7 \end{bmatrix}$。

任务

1. 确定 $k$ 的值，使得系统有唯一解。
2. 确定 $k$ 的值，使得系统有无穷多解。
3. 求矩阵 $A$ 的LU分解。
4. 写出系统的完整解。

解题过程

部分A：唯一解的条件

• 矩阵可逆性：矩阵 $A$ 有唯一解当且仅当 $A$ 是可逆的，即 $A$ 的秩为满秩（3）。
• 行操作：通过行操作将矩阵化为上三角形式。
  • 步骤1：从第二行减去第一行的1倍。
  • 步骤2：从第三行减去第一行的3倍。
  • 步骤3：从第三行减去第二行的1倍。
• 结果：最终矩阵为：

$$\begin{bmatrix} 1 & 1 & 1 & | & 2 \\ 0 & 1 & 2 & | & 1 \\ 0 & 0 & k-5 & | & 0 \\ \end{bmatrix}$$

• 结论：当 $k \neq 5$ 时，矩阵 $A$ 是满秩的，系统有唯一解。

部分B：无穷多解的条件

• 零空间非平凡：当 $k = 5$ 时，矩阵 $A$ 的秩为2，零空间非平凡。
• 结论：当 $k = 5$ 时，系统有无穷多解。

部分C：LU分解

• 矩阵 $U$：通过行操作得到的上三角矩阵 $U$ 为：

$$U = \begin{bmatrix} 1 & 1 & 1 \\ 0 & 1 & 2 \\ 0 & 0 & k-5 \\ \end{bmatrix}$$

• 矩阵 $L$：通过行操作的逆矩阵得到的下三角矩阵 $L$ 为：

$$L = \begin{bmatrix} 1 & 0 & 0 \\ -1 & 1 & 0 \\ -3 & 1 & 1 \\ \end{bmatrix}$$

部分D：完整解

• 当 $k \neq 5$ 时：
  • 解：通过回代法求解：

$$\mathbf{x} = \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix}$$

• 当 $k = 5$ 时：
  • 解： $x_3$ 是自由变量，设 $x_3 = c$：

$$\mathbf{x} = \begin{bmatrix} 1 \\ 1 - 2c \\ c \end{bmatrix}$$

---

第二部分：线性代数复习与练习

课程主题

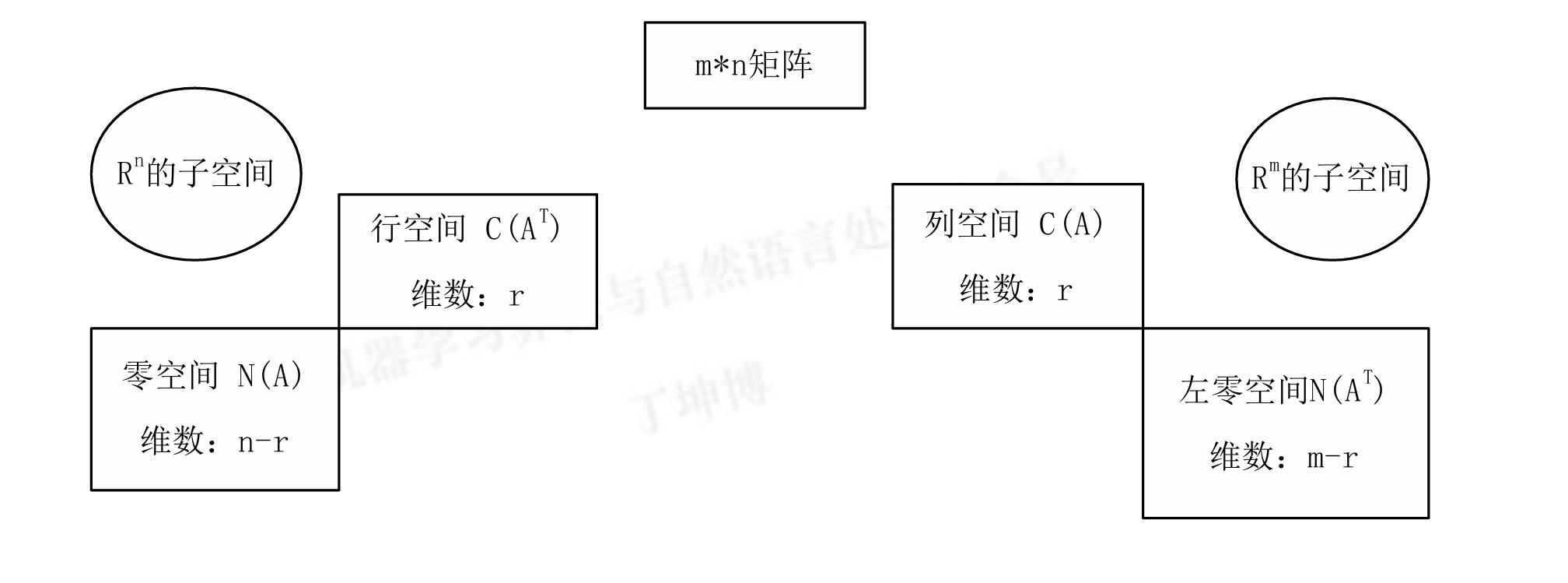
• 向量空间与子空间
• 矩阵的秩与零空间
• 线性系统的解法

练习题

题目1：向量空间的维度

问题：假设 $\mathbf{u}, \mathbf{v}, \mathbf{w}$ 是 $\mathbb{R}^7$ 中的非零向量，它们张成的子空间的可能维度是多少？
答案：可能的维度是1、2或3。因为只有三个向量，且它们非零。

题目2：矩阵的零空间

问题：给定一个5x3矩阵 $U$，其秩为3，求其零空间。
答案：零空间只包含零向量，因为秩为3，说明列向量线性无关。

题目3：矩阵的行操作

问题：给定一个10x3矩阵 $B$，由矩阵 $U$ 和 $2U$ 组成，求其行阶梯形式。
答案：行阶梯形式为：

$$\begin{bmatrix} U \\ 0 \\ \end{bmatrix}$$

因为 $U$ 已经是行阶梯形式，而 $2U$ 可以通过行操作消去。

题目4：矩阵的秩

问题：给定一个矩阵 $C$，由矩阵 $U$ 和 $-U$ 组成，求其秩。
答案：秩为6，因为 $U$ 的秩为3，而 $-U$ 不改变秩。

题目5：线性系统的解

问题：给定方程 $A \mathbf{x} = \begin{bmatrix} 2 \\ 4 \\ 2 \end{bmatrix}$，已知其完整解，求矩阵 $A$ 的秩。
答案：秩为1，因为零空间的维度为2，说明矩阵 $A$ 的秩为 $3 - 2 = 1$。

---

总结

• 线性方程组的解法：通过行操作将矩阵化为行阶梯形式，判断矩阵的秩。
• LU分解：将矩阵分解为下三角矩阵 $L$ 和上三角矩阵 $U$。
• 线性系统的完整解：包括特解和零空间的解。
• 矩阵的秩与零空间：秩为满秩时，系统有唯一解；秩不足时，系统可能有无穷多解或无解。

以下是将内容翻译为中文并优化解答过程后的Markdown格式内容：

MIT 18.06SC 第一单元考试解答

问题 1：矩阵方程 $Ax = b$

题目：
给定矩阵 $A$ 和向量 $b$，求解方程 $Ax = b$。

$$A = \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 1 & 1 \end{bmatrix}, \quad b = \begin{bmatrix} 1 \\ 0 \\ 1 \end{bmatrix}$$

解答：
通过行简化增广矩阵 $[A|b]$ 来求解方程 $Ax = b$。

$$\left[\begin{array}{ccc|c} 1 & 0 & 1 & 1 \\ 0 & 1 & 0 & 0 \\ 1 & 1 & 1 & 1 \end{array}\right]$$

1. 从第三行减去第一行：

$$\left[\begin{array}{ccc|c} 1 & 0 & 1 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{array}\right]$$

2. 从第三行减去第二行：

$$\left[\begin{array}{ccc|c} 1 & 0 & 1 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right]$$

由此可知，方程组简化为：

$$\begin{cases} x_1 + x_3 = 1 \\ x_2 = 0 \end{cases}$$

因此，解为：

$$x_1 = 1 - x_3, \quad x_2 = 0, \quad x_3 \text{ 为自由变量}$$

特解为：

$$x_p = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}$$

零空间的基为：

$$x_n = x_3 \begin{bmatrix} -1 \\ 0 \\ 1 \end{bmatrix}$$

因此，通解为：

$$x = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} + x_3 \begin{bmatrix} -1 \\ 0 \\ 1 \end{bmatrix}$$

问题 2：矩阵的零空间和列空间

题目：
给定矩阵 $A$，求其零空间和列空间。

$$A = \begin{bmatrix} 1 & 1 & 2 & 4 \\ 3 & 3 & 6 & 12 \\ 0 & 0 & 0 & 0 \end{bmatrix}$$

解答：

1. 零空间 $N(A)$：解方程 $Ax = 0$。

通过行简化 $A$：

$$\begin{bmatrix} 1 & 1 & 2 & 4 \\ 3 & 3 & 6 & 12 \\ 0 & 0 & 0 & 0 \end{bmatrix} \rightarrow \begin{bmatrix} 1 & 1 & 2 & 4 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix}$$

方程组简化为：

$$x_1 + x_2 + 2x_3 + 4x_4 = 0$$

设 $x_2 = s$，$x_3 = t$，$x_4 = u$ 为自由变量，则：

$$x_1 = -s - 2t - 4u$$

因此，零空间的基为：

$$N(A) = \text{span}\left\{ \begin{bmatrix} -1 \\ 1 \\ 0 \\ 0 \end{bmatrix}, \begin{bmatrix} -2 \\ 0 \\ 1 \\ 0 \end{bmatrix}, \begin{bmatrix} -4 \\ 0 \\ 0 \\ 1 \end{bmatrix} \right\}$$

2. 列空间 $C(A)$：列空间由 $A$ 的主列生成。

主列是第一列，因此：

$$C(A) = \text{span}\left\{ \begin{bmatrix} 1 \\ 3 \\ 0 \end{bmatrix} \right\}$$

问题 3：矩阵的逆和LU分解

题目：
给定矩阵 $A$，求其逆矩阵 $A^{-1}$，并进行LU分解。

$$A = \begin{bmatrix} 1 & 0 & 0 \\ 4 & 1 & 0 \\ 1 & 0 & 1 \end{bmatrix}$$

解答：

1. 求逆矩阵 $A^{-1}$：
   通过初等行变换将 $A$ 化为单位矩阵，同时对单位矩阵进行相同的变换。

$$\left[\begin{array}{ccc|ccc} 1 & 0 & 0 & 1 & 0 & 0 \\ 4 & 1 & 0 & 0 & 1 & 0 \\ 1 & 0 & 1 & 0 & 0 & 1 \end{array}\right]$$

1. 从第二行减去4倍的第一行：

$$\left[\begin{array}{ccc|ccc} 1 & 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & -4 & 1 & 0 \\ 1 & 0 & 1 & 0 & 0 & 1 \end{array}\right]$$

2. 从第三行减去第一行：

$$\left[\begin{array}{ccc|ccc} 1 & 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & -4 & 1 & 0 \\ 0 & 0 & 1 & -1 & 0 & 1 \end{array}\right]$$

因此，逆矩阵为：

$$A^{-1} = \begin{bmatrix} 1 & 0 & 0 \\ -4 & 1 & 0 \\ -1 & 0 & 1 \end{bmatrix}$$

2. LU分解：
   将 $A$ 分解为下三角矩阵 $L$ 和上三角矩阵 $U$。

$$A = LU$$

通过行变换，可以得到：

$$L = \begin{bmatrix} 1 & 0 & 0 \\ 4 & 1 & 0 \\ 1 & 0 & 1 \end{bmatrix}, \quad U = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$

因此，$A$ 的LU分解为：

$$A = LU = \begin{bmatrix} 1 & 0 & 0 \\ 4 & 1 & 0 \\ 1 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$

---

MIT 开放课程
http://ocw.mit.edu
18.06SC 线性代数，秋季 2011
有关引用这些材料或我们的使用条款的更多信息，请访问：http://ocw.mit.edu/terms