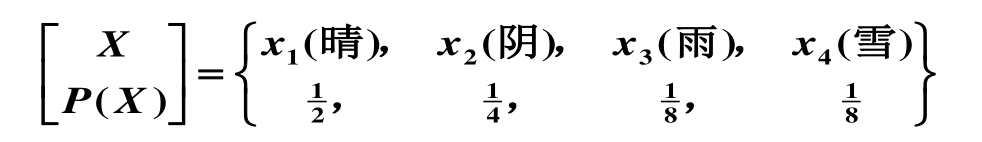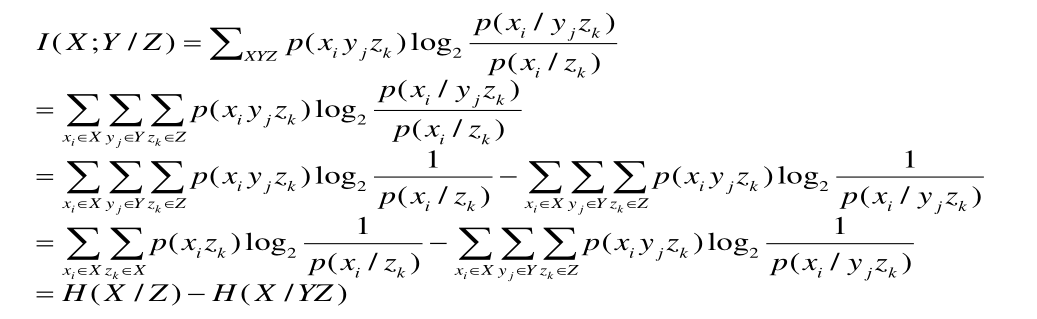- [ ] #### 3.1信道的数学模型及分类
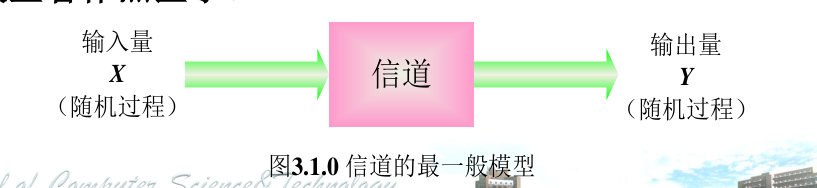
信道的数学模型
① 信道的广义性
- 信道本质上是一个有输入,有输出的系统
- 知道了信道的输入信号、输出信号以及它们之间的依赖关系,信道的全部特性就确定了。(BookxNote Pro📍)
② 一般信道的数学模型(BookxNote Pro📍)
- 知道了信道的输入信号、输出信号以及它们之间的依赖关系,信道的全部特性就确定了。(BookxNote Pro📍)
- 不研究信号在信道中传输的物理过程,把信道模型看作黑匣子。(BookxNote Pro📍)
- 本质上是视为一种黑箱,不去关注信道为什么产生,以及信道的性质,而是只关心统计特性
- 本质上是视为一种黑箱,不去关注信道为什么产生,以及信道的性质,而是只关心统计特性
(2) 信道的分类
① 根据输入输出随机信号的特点分类
- 看取值连续还是离散
(BookxNote Pro📍)
② 根据输入输出随机变量个数的多少分类(BookxNote Pro📍) - 根据符号的多少
③ 根据输入输出个数分类(BookxNote Pro📍) - 根据用户的多少来区别
④ 根据信道上有无干扰分类
⑤ 根据信道有无记忆特性分类
(5)离散信道的分类
根据信道统计特性(即p(x/y)),
离散信道又分为:◦
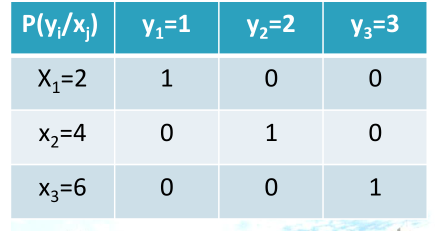
- 无干扰(无噪)信道◦
- 输出Y与输入X之间有确定的一一对应关系
- 有输入,那么输出一定是知道的
- 有干扰无记忆信道
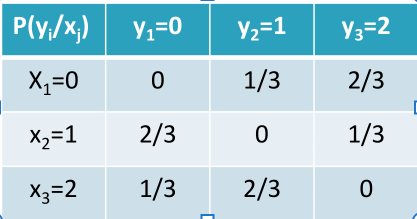
- 有干扰:信道输出符号与输入符号间无确定的对应关系
- 无记忆:任意时刻输出符号只依赖于对应时刻的输入符号,
- 有干扰有记忆信道(BookxNote Pro📍)
- 处理方式:
- 将记忆性较强的N个符号作为一个矢量符号处理,各矢量符号间认为是无记忆的
- 马尔科夫链
- 处理方式:
平均互信息和平均条件互信息
(1) 互信息量和条件互信息量
- 最简单的通信系统模型:
- X—信源发出的离散消息集合
- Y—信宿收到的离散消息集合◦
- 信源通过有干扰的信道发出消息传递给信宿;
- 信宿事先不知道某一时刻发出的是哪一个消息,所以每个消息是随机事件的一个结果。(BookxNote Pro📍)
互信息量的定义
- 先验概率:信源发出消息 xi 的概率 p(xi)。
- 后验概率:信宿收到 yj后推测信源发出 xi 的概率:
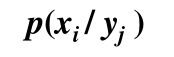
- 互信息量:yj对 xi 的互信息量定义为后验概率与先验概率比值的对数。
- 本质上是后验概率与先验概率只差,也就是不确定性的减少
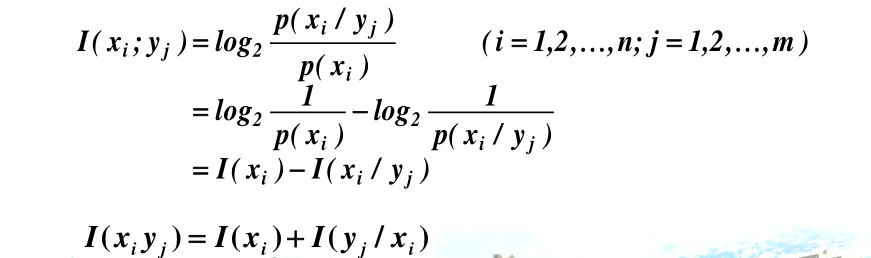
- 本质上是后验概率与先验概率只差,也就是不确定性的减少
互信息量举例
某地二月份天气构成的信源为:
- 先验概率
- 后验概率
- 互信息量
- 结果表明从 y1 分别得到了 x2,x3,x4 各 1 比特的信息量;
- ◦ 或者说 y1使 x2,x3,x4 的不确定度各减少量 1 比特。(BookxNote Pro📍)
互信息量的不同表达式
- 观察者站在输出端
- 自信息量:对 yj一无所知的情况下 xi 存在的不确定度;
- 条件自信息量:已知 yj的条件下 xi仍然存在的不确定度;
- 互信息量:两个不确定度之差是不确定度被消除的部分,即等于自信息量减去条件自信息量。(BookxNote Pro📍)
互信息的性质
- 对称性
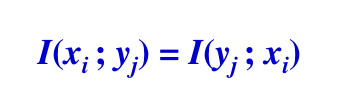
- 我们可以将输入与输出视为两个信源,无论哪个作为输出,哪个作为输入,都是可以的,只是视角的不同
- 独立性
-
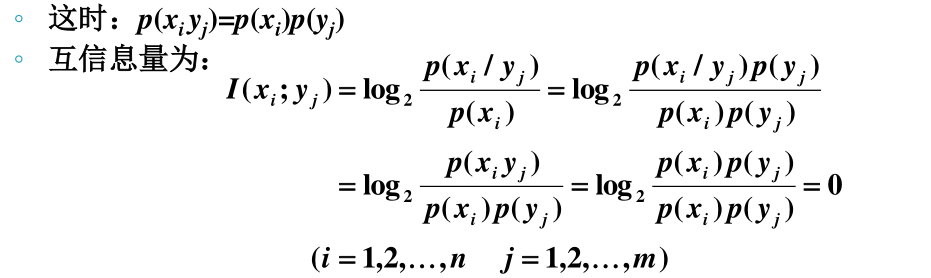
-
表明 xi 和 yj之间不存在统计约束关系,从 yj得不到关于的 xi 任何信息,反之亦然。(BookxNote Pro📍)
-
条件互信息量

平均互信息量
平均互信息量定义:互信息量 I(xi;yj) 在联合概率
空间P(XY) 中的统计平均值(简称平均互信息/平
均交互信息量/交互熵)
- 平均接收到一个符号减少的不确定性
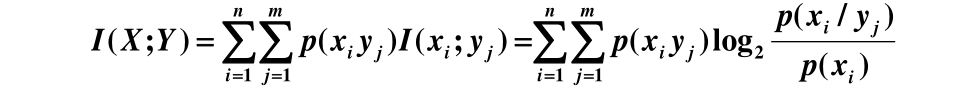
平均互信息量的物理含义
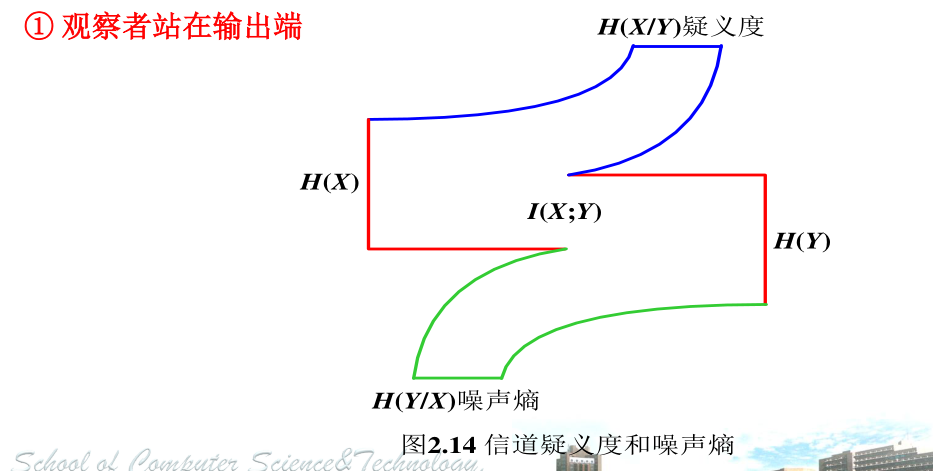
① 观察者站在输出端
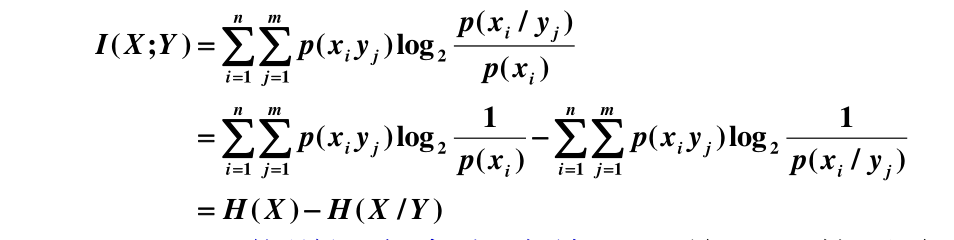
-
H(X/Y) —信道疑义度/损失熵。 Y 关于 X 的后验不确定度。表示收到变量Y 后,对随机变量 X 仍然存在的不确定度。代表了在信道中损失的信息
-
H(X) —X 的先验不确定度/无条件熵。
-
I(X;Y)—收到 Y 前、后关于 X 的不确定度减少的量。从 Y 获得的关于 X 的平均信息量。
② 观察者站在输入端
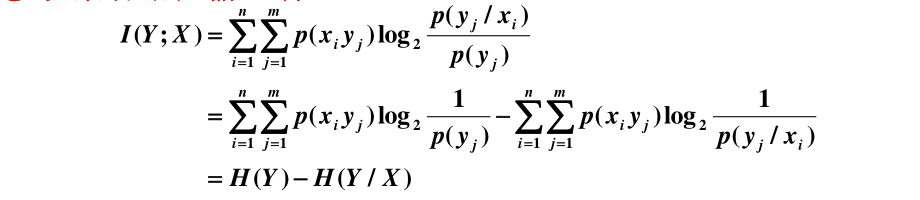
-
H(Y/X)—噪声熵:表示发出随机变量 X 后,对随机变量 Y 仍然存在的平均不确定度。如果信道中不存在任何噪声,发送端和接收端必存在确定的对应关系,发出 X 后必能确定对应的 Y,而现在不能完全确定对应的Y,这显然是由信道噪声所引起的。
-
I(Y;X) —发出 X 前、后关于 Y 的先验不确定度减少的量。
③ 观察者站在通信系统总体立场上
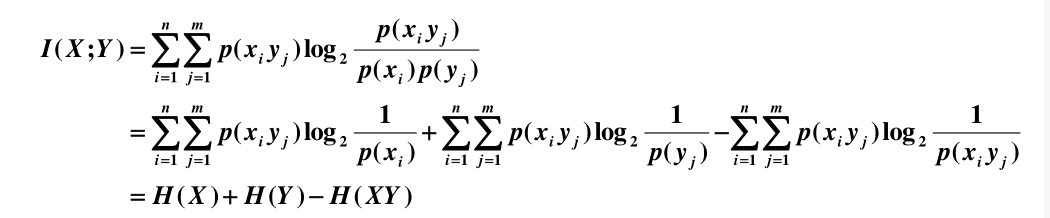
-
H(XY)—联合熵:表示输入随机变量 X,经信道传输到达信宿,输出随机变量 Y。即收、发双方通信后,整个系统仍然存在的不确定度。
-
I(X;Y) —通信前、后整个系统不确定度减少量。
-
在通信前把 X 和 Y 看成两个相互独立的随机变量,整个系统的先验不确定度为 X 和Y 的联合熵 H(X)+H(Y);
-
通信后把信道两端出现 X 和 Y 看成是由信道的传递统计特性联系起来的、具有一定统计关联关系的两个随机变量,这时整个系统的后验不确定度由 H(XY) 描述。
平均条件互信息量
- 平均条件互信息 I(X;Y/Z) 克服了互信息量 I(xi;yj/zk) 的随机性,成为一个确定的量。
- 含义:在已知Z条件下,每接收到Y中一个符号后平均获得的关于X的信息量,等于已知Z条件下信源X中每符号平均信息量减去已知YZ同时发生情况下,信源X中每符号的平均信息量。