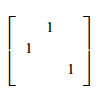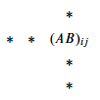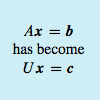看世界，看自己
  文章分类
FREERTOS 1 操作系统 11 深度学习 6 数据结构与算法 3 数学 15 信息论 2 英语 42 计算机组成原理 4 计算机网络 1 工具 2 阅读 2 移动通信原理 1
【MIT线性代数】【exam1】 【MIT线性代数】【exam1】
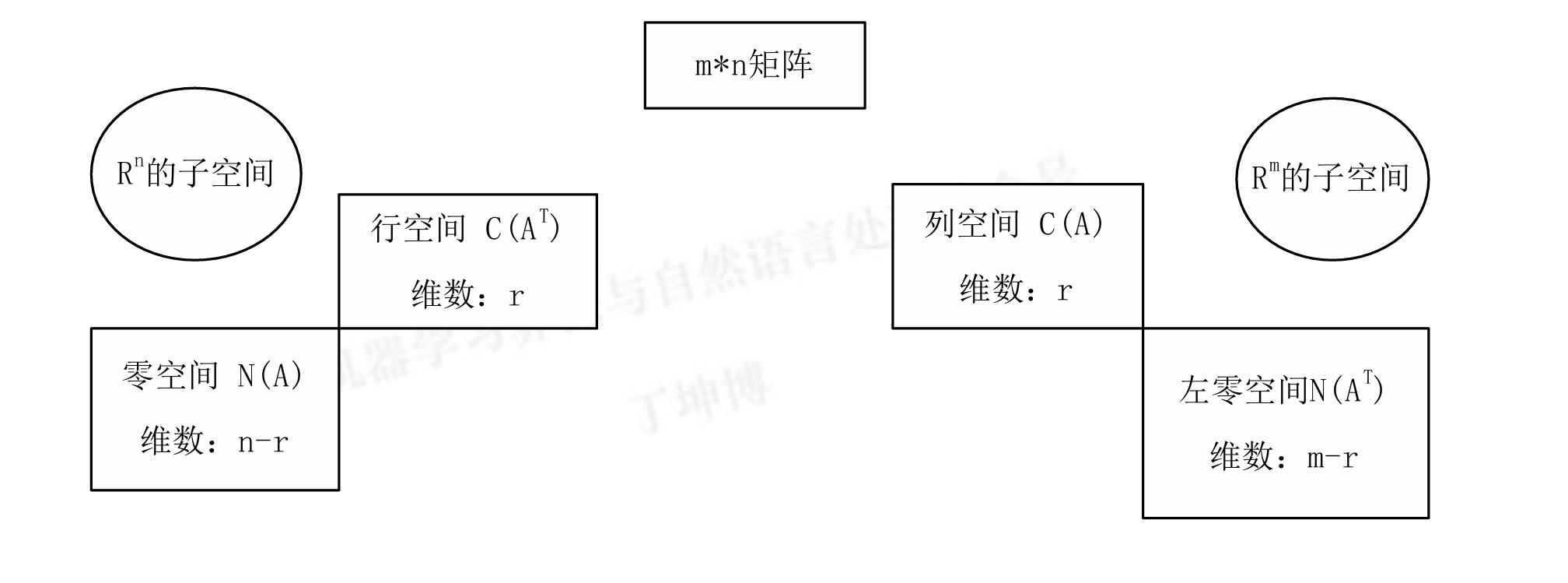
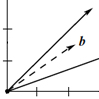
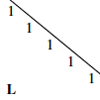
18.065C 第一单元考试解答 问题 1 (24 分) 这个问题是关于一个 m×nm \times nm×n 矩阵 AAA，其中： Ax=[111] 无解，且 Ax=[010] 有唯一解。A x = \b
2025-03-22 数学
MIT18.06SC 2011fall 线性代数 problem-sets exam
【MIT线性代数】【lec13】第一单元复习 【MIT线性代数】【lec13】第一单元复习
第一部分：线性方程组的解法与LU分解 课程主题 线性方程组的解法 矩阵的LU分解 线性系统的完整解 问题描述 给定一个3x3矩阵 AAA，其中最后一个元素是参数 kkk。矩阵 AAA 如下： A=[11112334k]A = \b
2025-03-19 数学
MIT18.06SC 2011fall 线性代数 problem-sets
【MIT线性代数】【lec12】 图与矩阵 【MIT线性代数】【lec12】 图与矩阵
线性代数应用：图与矩阵 1. 线性代数的应用背景 线性代数中的矩阵并非随意构造，而是来源于实际应用。例如，化学教授通过矩阵分析化学反应，利用行简化（row reduction）来理解复杂的化学反应过程。 在Mathworks（Matl
2025-03-18 数学
MIT18.06SC 2011fall 线性代数 problem-sets
【MIT线性代数】【lec6】列空间与零空间 【MIT线性代数】【lec6】列空间与零空间
线性代数笔记：第六讲 - 向量空间与子空间 1. 向量空间的定义 定义：向量空间是一组向量，满足以下两个条件： 可以将其中任意两个向量相加，结果仍在该空间内。 可以将其中任意一个向量乘以任意常数，结果仍在该空间内。 线性组合：上
2025-03-12 数学
MIT18.06SC 2011fall 线性代数 problem-sets
【MIT线性代数】【lec5】置换矩阵、转置矩阵与向量空间 【MIT线性代数】【lec5】置换矩阵、转置矩阵与向量空间
线性代数第五讲：置换矩阵、转置矩阵与向量空间 一、置换矩阵（Permutations） 1. 置换矩阵的定义 定义：置换矩阵 PPP 是通过交换单位矩阵 III 的行得到的矩阵。 性质： 置换矩阵的逆矩阵等于其转置矩阵，即 P−1
2025-03-12 数学
MIT18.06SC 2011fall 线性代数 problem-sets
【MIT线性代数】【lec4】分解为a = lu 【MIT线性代数】【lec4】分解为a = lu
线性代数第四讲：矩阵乘法与逆矩阵 一、矩阵乘法与逆矩阵 1. 矩阵乘法的逆 问题：已知矩阵 AAA 和 BBB 的逆矩阵，求 ABABAB 的逆矩阵。 结论：(AB)−1=B−1A−1(AB)^{-1} = B^{-1}A^{-1}
2025-03-12 数学
MIT18.06SC 2011fall 线性代数 problem-sets
【MIT线性代数】【lec3】矩阵乘法与逆矩阵 【MIT线性代数】【lec3】矩阵乘法与逆矩阵
线性代数第三讲：矩阵乘法与逆矩阵 一、矩阵乘法 1. 标准乘法规则 定义：矩阵 AAA 乘以矩阵 BBB 得到矩阵 CCC。 元素计算：矩阵 CCC 的第 iii 行第 jjj 列的元素 cijc_{ij}cij​ 是 AAA 的第
2025-03-12 数学
MIT18.06SC 2011fall 线性代数 problem-sets
【MIT线性代数】【lec2】消元法与矩阵运算 【MIT线性代数】【lec2】消元法与矩阵运算
线性代数第二讲：消元法与矩阵运算 一、消元法（Elimination） 1. 消元法概述 目标：通过逐步消元将线性方程组化为上三角形式（Upper Triangular Form），从而简化求解过程。 方法：从第一个方程开始，逐步消
2025-03-12 数学
MIT18.06SC 2011fall 线性代数 problem-sets
【MIT线性代数】【lec1】 线性方程组的几何与代数视角 【MIT线性代数】【lec1】 线性方程组的几何与代数视角
线性代数第一讲：线性方程组的几何与代数视角 一、课程介绍 课程名称：18.06 线性代数 教材：《Introduction to Linear Algebra》 课程网址：web.mit.edu/18.06 主讲人：Gilbert S
2025-03-12 数学
MIT18.06SC 2011fall 线性代数 problem-sets
【MIT线性代数】【lec11】 向量空间、矩阵秩与图 【MIT线性代数】【lec11】 向量空间、矩阵秩与图
线性代数第十一讲：矩阵空间、子空间与秩 一、矩阵空间与子空间 1. 矩阵空间 MMM 定义：所有 3×33 \times 33×3 矩阵构成的空间。 性质：可以进行矩阵加法和数乘，但不涉及矩阵乘法。 矩阵也可以视为向量元素 维
2025-03-12 数学
MIT18.06SC 2011fall 线性代数 problem-sets
1 / 2