看世界，看自己
  文章分类
FREERTOS 1 操作系统 11 深度学习 6 数据结构与算法 3 数学 15 信息论 2 英语 42 计算机组成原理 4 计算机网络 1 工具 2 阅读 2 移动通信原理 1
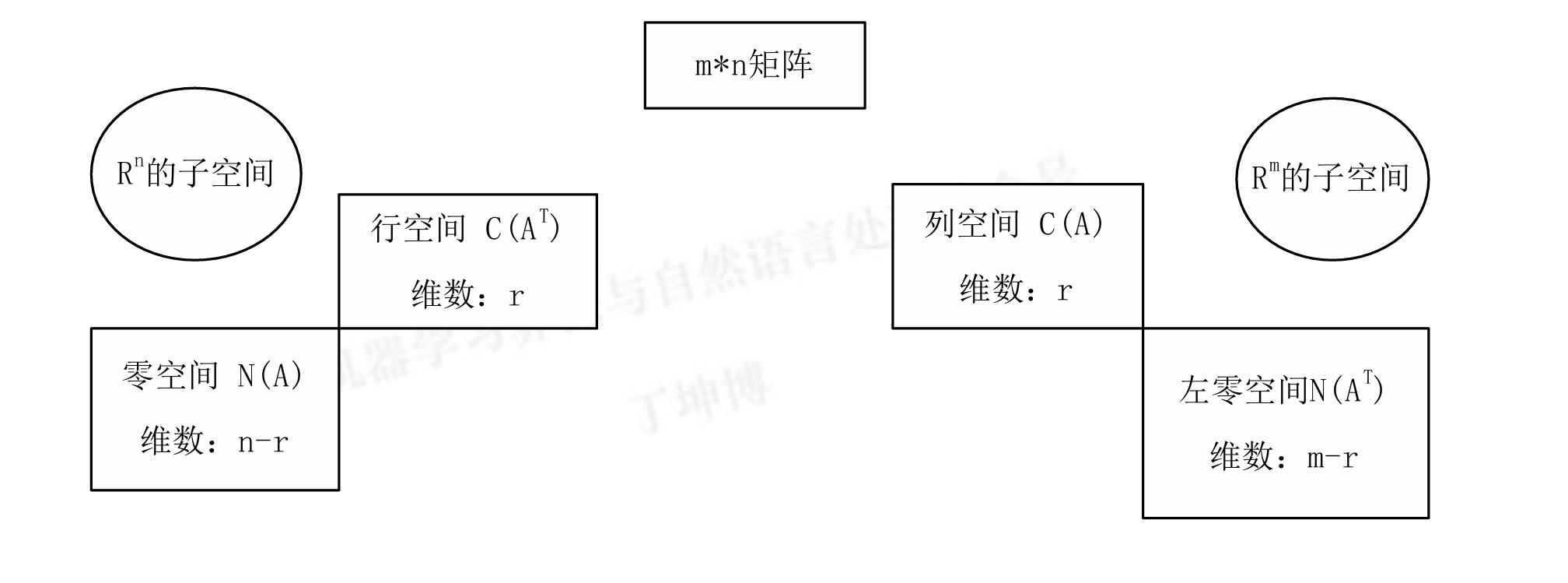
【MIT线性代数】【番外review】向量、矩阵与子空间 【MIT线性代数】【番外review】向量、矩阵与子空间
线性代数复习：向量、矩阵与子空间 一、线性代数的重要性 教授观点：Gilbert Strang 教授认为线性代数非常重要，而美国大学通常过于注重微积分和微分方程的教学，导致学生在实际计算中缺乏线性代数的训练。 实际应用：在现实世界中，
2025-03-12 数学
MIT18.06SC 2011fall 线性代数 problem-sets
【MIT线性代数】【lec9】线性独立性、基和维度 【MIT线性代数】【lec9】线性独立性、基和维度
线性代数笔记 - 第九讲：线性独立性、基和维度 一、课程主题 本次课程的核心内容是线性代数中的几个重要概念：线性独立性（Linear Independence）、向量张成空间（Span）、基（Basis） 和 维度（Dimension）
2025-03-12 数学
MIT18.06SC 2011fall 线性代数 problem-sets
【MIT线性代数】【lec8】求解ax=b以及行化简 【MIT线性代数】【lec8】求解ax=b以及行化简
线性代数笔记 - 第八讲：解线性方程组 Ax=b 一、课程主题 本次课程的目标是完全解决线性方程组 Ax=bAx = bAx=b 的问题，包括判断方程组是否有解，以及如何找到所有解。 二、解线性方程组的步骤 （一）判断方程组是否有解
2025-03-12 数学
MIT18.06SC 2011fall 线性代数 problem-sets
【MIT线性代数】【lec7】求解ax=0以及子空间 【MIT线性代数】【lec7】求解ax=0以及子空间
线性代数笔记 - 第七讲 一、课程主题 本次课程主要探讨了线性代数中的向量空间，特别是矩阵的零空间（Null Space）和列空间（Column Space），并详细介绍了如何描述和计算这些空间中的向量。 二、矩阵的零空间 （一）零
2025-03-12 数学
MIT18.06SC 2011fall 线性代数 problem-sets
【MIT线性代数】【lec10】 矩阵的四个基本子空间 【MIT线性代数】【lec10】 矩阵的四个基本子空间
线性代数第十讲：矩阵的四个基本子空间 一、课程回顾与修正 回顾：上一讲中，我们讨论了矩阵的列空间和零空间。 修正：在上一讲中，我犯了一个错误。我选择了向量 [1, 1, 2] 和 [2, 2, 5] 作为基，并试图加入 [3, 3,
2025-03-12 数学
MIT18.06SC 2011fall 线性代数 problem-sets
2 / 2